早教吧作业答案频道 -->数学-->
如图,点C是以AB为直径的O上一点,CD是O切线,D在AB的延长线上,作AE⊥CD于E.(1)求证:AC平分∠BAE;(2)若AC=2CE=6,求O的半径;(3)请探索:线段AD,BD,CD之间有何数量关系?请证明
题目详情
如图,点C是以AB为直径的 O上一点,CD是 O切线,D在AB的延长线上,作AE⊥CD于E.
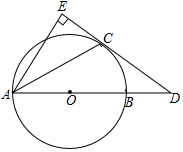
(1)求证:AC平分∠BAE;
(2)若AC=2CE=6,求 O的半径;
(3)请探索:线段AD,BD,CD之间有何数量关系?请证明你的结论.

(1)求证:AC平分∠BAE;
(2)若AC=2CE=6,求 O的半径;
(3)请探索:线段AD,BD,CD之间有何数量关系?请证明你的结论.
▼优质解答
答案和解析
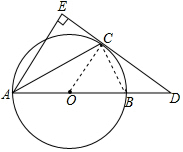 (1)证明:连接OC,
(1)证明:连接OC,
∵CD是 O切线,
∴OC⊥CD,
∵AE⊥CD,
∴OC∥AE,
∴∠EAC=∠ACO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠EAC=∠A=CAO,
即AC平分∠BAE;
(2) 连接BC,
∵AE⊥CE,AC=2CE=6,
∴sin∠CAE=
=
,
∴∠CAE=30°,
∴∠CAB=∠CAE=30°,
∵AB是 O的直径,
∴∠ACB=90°,
∴cos∠CAB=
=
,
∴AB=4
,
∴ O的半径是2
;
(3)CD2=BD•AD,
证明:∵∠DCB+∠BCO=90°,∠ACO+∠BCO=90°,
∴∠DCB=∠ACO,
∴∠DCB=∠ACO=∠CAD,
∵∠D=∠D,
∴△BCD∽△CAD,
∴
=
,
即CD2=BD•AD.
 (1)证明:连接OC,
(1)证明:连接OC,∵CD是 O切线,
∴OC⊥CD,
∵AE⊥CD,
∴OC∥AE,
∴∠EAC=∠ACO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠EAC=∠A=CAO,
即AC平分∠BAE;
(2) 连接BC,
∵AE⊥CE,AC=2CE=6,
∴sin∠CAE=
| CE |
| AC |
| 1 |
| 2 |
∴∠CAE=30°,
∴∠CAB=∠CAE=30°,
∵AB是 O的直径,
∴∠ACB=90°,
∴cos∠CAB=
| AC |
| AB |
| ||
| 2 |
∴AB=4
| 3 |
∴ O的半径是2
| 3 |
(3)CD2=BD•AD,
证明:∵∠DCB+∠BCO=90°,∠ACO+∠BCO=90°,
∴∠DCB=∠ACO,
∴∠DCB=∠ACO=∠CAD,
∵∠D=∠D,
∴△BCD∽△CAD,
∴
| BD |
| CD |
| CD |
| AD |
即CD2=BD•AD.
看了 如图,点C是以AB为直径的O...的网友还看了以下:
点C在以AB为直径的半圆上,∠CAB的平分线AD交BC于点D,⊙O经过A D两点,且圆心O在AB上 2020-05-15 …
O'在圆O上,以O'为圆心的圆交O'于A,B,圆O的弦O'C交圆O;于D,求证D为三角形abc内心 2020-06-02 …
··一道简单的数学题,先到的.对的.角D=90度,BD=CD,BO是角DBC的角平分线,CE垂直B 2020-06-03 …
已知圆心角的度数,求弦长例1、如图,点O是∠EPF的平分线上一点,以O为圆心的圆和角的两边所在的直 2020-06-03 …
AB是圆O的直径AB=6角CAD=30度,求弦长DCOA是圆O的半径,以OA为直径的圆C与圆O的弦 2020-06-06 …
已知函数f(x)在定义域R上可导,设点P是函数y=f(x)是图象上距离原点O最近的点.(1)若点P 2020-06-14 …
三角形ABC内接于圆o,AM平分角BAC交圆O于M点,AD垂直BC于D.求证:角MAO=角MAD有 2020-06-22 …
我国境内的股票价格指数不包括( )。A.沪深300指数B.恒生指数C.上证综合指数D.深证综合 2020-06-27 …
下列各组词语中加点字的读音,全都正确的一组是()A.着陆(zháo)模具(mú)通缉令(jī)岁稔年 2020-12-14 …
记账凭证应具有的共同的基本内容包括()。A.填制凭证的日期和凭证的编号B.会计科目的名称、记账方向和 2020-12-15 …