早教吧作业答案频道 -->数学-->
如图1,△ABC的两条中线AD、BE相交于点O(1)求证:DO:AO=1:2;(2)连接CO并延长交AB于F,求证:CF也是△ABC的中线;(3)在(2)中,若∠A=90°,其它条件不变,连接DF交BE于K(如图2),连
题目详情
如图1,△ABC的两条中线AD、BE相交于点O
(1)求证:DO:AO=1:2;
(2)连接CO并延长交AB于F,求证:CF也是△ABC的中线;
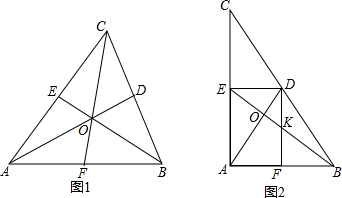
(3)在(2)中,若∠A=90°,其它条件不变,连接DF交BE于K(如图2),连接ED,且△EDK∽△CAB,求AC:AB的值.
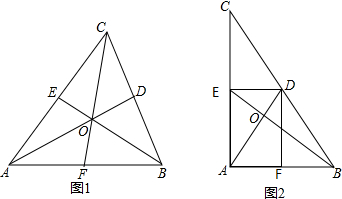
(1)求证:DO:AO=1:2;
(2)连接CO并延长交AB于F,求证:CF也是△ABC的中线;
(3)在(2)中,若∠A=90°,其它条件不变,连接DF交BE于K(如图2),连接ED,且△EDK∽△CAB,求AC:AB的值.

▼优质解答
答案和解析
 (1)证明:连接ED,
(1)证明:连接ED,
∵E、D分别为AC、BC的中点,
∴ED∥AB,且ED=
AB,
∴△EDO∽△BAO,
∴DO:AO=ED:AB=1:2;
(2)证明:设CF交ED于点G,
由△DGO∽△AFO,得到DG:AF=DO:AO=1:2,
由DG∥AB得DG:BF=CD:CB=1:2,
∴DG:AF=DG:BF,
∴AF=BF,
∴AF也是△ABC的中线;
(3) 由∠A=90°,得到四边形AFDE是矩形,
∴△EDK∽△BAE,
∵△EDK∽△CAB,
∴△BAE∽△CAB,
∴AE:AB=AB:AC,
∵AE=
AC,
∴AC:AB=
.
 (1)证明:连接ED,
(1)证明:连接ED,∵E、D分别为AC、BC的中点,
∴ED∥AB,且ED=
| 1 |
| 2 |
∴△EDO∽△BAO,
∴DO:AO=ED:AB=1:2;
(2)证明:设CF交ED于点G,
由△DGO∽△AFO,得到DG:AF=DO:AO=1:2,
由DG∥AB得DG:BF=CD:CB=1:2,
∴DG:AF=DG:BF,
∴AF=BF,
∴AF也是△ABC的中线;
(3) 由∠A=90°,得到四边形AFDE是矩形,
∴△EDK∽△BAE,
∵△EDK∽△CAB,
∴△BAE∽△CAB,
∴AE:AB=AB:AC,
∵AE=
| 1 |
| 2 |
∴AC:AB=
| 2 |
看了 如图1,△ABC的两条中线A...的网友还看了以下:
1.什么叫从集合a到集合b的函数?2.判断下列是不是从集合a到集合b的函数题1--a={1/2,1 2020-05-13 …
已知A,B,C,D,E,F是含有同一种元素的化合物,其中F能使红色石蕊试纸变蓝色,它们之间能发生如 2020-05-20 …
已知f(x+1)是偶函数,当1<x1<x2时,f(x2)-f(x1)]*(x2-x1)>0恒成立, 2020-05-22 …
要高考了,问一下,f(a+x)=f(a-x)等价于f(2a-x)=f(x),可以推出T=2a和对称 2020-06-10 …
已知集合A={1,2,3},B={-1,o,1}已知集合A={1,2,3},B={-1,0,1}, 2020-07-30 …
已知数集A中有5个元素,数集B中有3个元素,若集合B中的元素在A中都有元素和它对应,且满足f(a1 2020-07-30 …
f(x+3)=-f(3-x)表示的意思为什么是函数f(x)以点(3,0)为对称中心呢.为什么不是表 2020-08-01 …
f(x)是定义域为R的奇函数,它的最小正周期为2,则:f(1)+f(2)+f(3)…+f(1995 2020-08-03 …
时间很赶,1.设函数y=x^2-3|x-1|-1的图像与x轴的焦点个数有()A.1个B.2个C.3个 2020-11-10 …
几个反函数的题目1一个函数图像过2.3象限,那它的反函数过几象限?2已知ax+2的反函数是3x-b, 2020-12-08 …