设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则r=2Sa+b+c，类比这个结论可知：四面体S-ABC的四个面的面积分别为S1、S2、S3、S4，内切球半径为R，四面体S-ABC的体积为V，则R=

Question

设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则r=

(2S)/(a+b+c)，类比这个结论可知：四面体S-ABC的四个面的面积分别为S₁、S₂、S₃、S₄，内切球半径为R，四面体S-ABC的体积为V，则R=（　　）

A.

(V)/(S1+S2+S3+S4)

B.

(2V)/(S1+S2+S3+S4)

C.

(3V)/(S1+S2+S3+S4)

D.

(4V)/(S1+S2+S3+S4)

Answer 1

设四面体的内切球的球心为O，
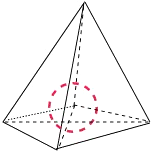
则球心O到四个面的距离都是R，
所以四面体的体积等于以O为顶点，
分别以四个面为底面的4个三棱锥体积的和．
则四面体的体积为 V四面体A-BCD=(1)/(3)(S1+S2+S3+S4)R
∴R=(3V)/(S1+S2+S3+S4)
故选C．