（12分）一根内径均匀，一端封闭，另一端开口的直玻璃管，长l=100cm，用一段长h=25cm的水银柱将一部分空气封在管内，将其开口朝上竖直放置，被封住的气柱长l0=62

Question

（ 12 分） 一根内径均匀，一端封闭，另一端开口的直玻璃管，长 l=100cm ，用一段长 h=25cm 的水银柱将一部分空气封在管内，将其开口朝上竖直放置，被封住的气柱长 l ₀ =62.5cm 。这时外部的大气压 p ₀ =75cmHg 环境温度 t ₀ = － 23 ℃ ，见下图，现在使气柱温度缓慢地逐渐升高，外界大气压保持不变，试分析为保持管内被封气体具有稳定的气柱长，温度能升高的最大值，并求出这个温度下气柱的长。

Answer 1

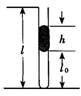
解析：

这是一个关于气体在状态变化过程中，状态参量存在极值的问题，首先，对过程进行分析，当管内气体温度逐渐升高时，管内气体体积要逐渐增大，气体压强不变， pV 值在增大。当上水银面升到管口时，水银开始从管内排出，因为 =C ，当管内水银开始排出后，空气柱体积增大，而压强减小，若 pV 值增大，则温度 T 继续升高，当 pV 值最大时温度最高。如果温度再升高不再满足 =C ，管内气体将不能保持稳定长度。

选取封闭气体为研究对象，在温度升高过程中，可分成两个过程研究。

第一过程：从气体开始升温到水银升到管口，此时气体温度为 T ，管的横截面积为 S ，此过程为等压过程，根据盖 ・ 吕萨克定律有：

= 所以 T= T ₀

其中： T ₀ =t ₀ +273=250K   l′=75cm   l ₀ =62.5cm 。

代入数据解得 T=300 （ K ）

第二过程，温度达到 300K 时，若继续升温，水银开始溢出，设当温度升高到 T′ 时，因水银溢出使水银减短了 x ，此过程气体的三个状态参量 p 、 V 、 T 均发生了变化。 p ₁ =p ₀ +h=75+25=100 （ cmHg ）   V ₁ =l′s=7.5S

T ₁ =300K

p ₂ = （ p ₀ +h － x ） = （ 100 － x ） cmHg   V ₂ = （ 75+x ） S

T ₂ =?

根据状态方程 = 则有

=

所以 T ₂ = （ 100 － x ）（ 75+x ） = － x ₂ +x+300

根据数学知识得   当 x=12.5m 时   T ₂ 取得最大值，且最大值 T _2max =306.25K 即当管内气体温度升高到 T _2max =33.25 ℃ 时，管内气柱长为 87.5cm 。