已知椭圆E：（a＞b＞0）的离心率，且点在椭圆E上．（Ⅰ）求椭圆E的方程；（Ⅱ）直线l与椭圆E交于A、B两点，且线段AB的垂直平分线经过点．求△AOB（O为坐标原点）面积的最大值．

Question

已知椭圆E：（a＞b＞0）的离心率，且点在椭圆E上．

（Ⅰ）求椭圆E的方程；

（Ⅱ）直线l与椭圆E交于A、B两点，且线段AB的垂直平分线经过点．求△AOB（O为坐标原点）面积的最大值．

Answer 1

【考点】椭圆的简单性质．

【分析】（Ⅰ）运用离心率公式和点满足椭圆方程，解方程可得a，b，进而得到椭圆方程；

（Ⅱ）设A（x₁，y₁），B（x₂，y₂），讨论直线AB的斜率为0和不为0，联立直线方程和椭圆方程，运用韦达定理和弦长公式，结合基本不等式和二次函数的最值的求法，可得面积的最大值．

【解答】（Ⅰ）由已知，e==，a²﹣b²=c²，

∵点在椭圆上，

∴，解得a=2，b=1．

∴椭圆方程为；

（Ⅱ）设A（x₁，y₁），B（x₂，y₂），

∵AB的垂直平分线过点，∴AB的斜率k存在．

当直线AB的斜率k=0时，x₁=﹣x₂，y₁=y₂，

∴S_△AOB=•2|x|•|y|=|x|•

=≤•=1，

当且仅当x₁²=4﹣x₁²，取得等号，

∴时，（S_△AOB）_max=1；

当直线AB的斜率k≠0时，设l：y=kx+m（m≠0）．

消去y得：（1+4k²）x²+8kmx+4m²﹣4=0，

由△＞0可得4k²+1＞m²①，

x₁+x₂=﹣，x₁x₂=，可得，

，

∴AB的中点为，

由直线的垂直关系有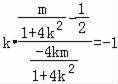，化简得1+4k²=﹣6m②

由①②得﹣6m＞m²，解得﹣6＜m＜0，

又O（0，0）到直线y=kx+m的距离为，

，

=，

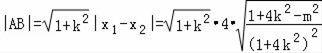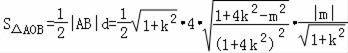
∵﹣6＜m＜0，∴m=﹣3时，．

由m=﹣3，∴1+4k²=18，解得；

即时，（S_△AOB）_max=1；       

综上：（S_△AOB）_max=1．

【点评】本题考查椭圆的方程的求法，注意运用离心率公式和点满足椭圆方程，考查三角形的面积的最值的求法，注意运用联立直线方程和椭圆方程，运用韦达定理和弦长公式，以及基本不等式，考查化简整理的运算能力，属于中档题．