已知椭圆x2a2+y2b2=1（a>b>0）的左、右焦点分别为F1，F2，过F1且与x轴垂直的直线交椭圆于A、B两点，直线AF2与椭圆的另一个交点为C，若S△ABC=3S△BCF2，则椭圆的离心率为（）A.55B.33C.

Question

已知椭圆

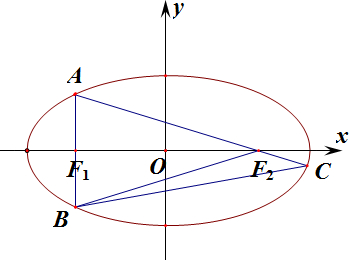
(x2)/(a2)+(y2)/(b2)=1（a>b>0）的左、右焦点分别为F₁，F₂，过F₁且与x轴垂直的直线交椭圆于A、B两点，直线AF₂与椭圆的另一个交点为C，若S△ABC=3S△BCF2，则椭圆的离心率为（　　）

A.

(√(5))/(5)

B.

(√(3))/(3)

C.

(√(10))/(5)

D.

(3√(3))/(10)

Answer 1

椭圆(x2)/(a2)+(y2)/(b2)=1（a>b>0）焦点在x轴上，设椭圆的左、右焦点分别为F₁（-c，0），F₂（c，0），
由x=-c，代入椭圆方程可得y=±(b2)/(a)，可设A（-c，(b2)/(a)），C（x，y），
由S△ABC=3S△BCF2，
可得

AF2

=2

F2C

，即有（2c，-(b2)/(a)）=2（x-c，y），即2c=2x-2c，(b2)/(a)=2y，
可得：x=2c，y=-(b2)/(2a)，
代入椭圆方程可得：(4c2)/(a2)+(b2)/(4a2)=1，由b²=a²-c²，根据离心率公式可知：e=(c)/(a)，
整理得：16e²+1-e²=4，解得e=±(√(5))/(5)，
由0<e<1，则e=(√(5))/(5)，
故选A．