已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且当PA与抛物线相切时,点P恰好在以A、B为焦点的双曲线上,则双曲线的离心率为()A.5-12B.2+12C.2+1D.5
已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且当PA与抛物线相切时,点P恰好在以A、B为焦点的双曲线上,则双曲线的离心率为( )
A.
-15 2
B.
+12 2
C.
+12
D.
-15
设直线AP的方程为y=kx-1,
|
∴△=16k2-16=0,
∴k=±1,
∴P(2,1),
∴双曲线的实轴长为丨PA丨-丨PB丨=2(
| 2 |
| 2 |
∴双曲线的离心率为e=
| c |
| a |
| 1 | ||
|
| 2 |
则双曲线的离心率
| 2 |
故选C.
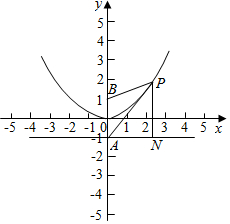
已知椭圆C:x^2/a^2+y^2/b^2=1(a>b>0)的离心率为√6/3,短轴的一个端点到右 2020-05-16 …
已知一个圆和Y轴相切,在直线y=x上截得弦长为2√7,且圆心在直线x-3y=0上,求圆的方程.因为 2020-05-16 …
已知椭圆X^2/a^2+y^2/b^2=1上任意一点M与短轴两端点B1,B2的连线分别与X轴交于P 2020-05-20 …
直线y=ax+b向y轴负方向移动1新的直线方程是什么?圆(x-a)^2+(y-b)^2=r^2,圆 2020-05-22 …
()是一种以内孔为基准装夹达到相对位置精度的装夹方法A.心轴B.平口钳C.俩顶尖D.一夹一顶 2020-06-07 …
点M是椭圆X^2/a^+Y^2/b^=1(a>b>0)上的点已知点M在椭圆x^2/a^2+y^2/ 2020-06-21 …
从椭圆X^2/A^2+Y^2/B^2=1(A>B>0)上的一点P向X轴做垂线,垂足恰为左焦点F1. 2020-06-21 …
长轴在x轴上的椭圆x^2/a^2+y^2/b^2=1...急)长轴在x轴上的椭圆(x^2/a^2) 2020-07-16 …
已知椭圆C1:已知椭圆C1:x^2/a^2+y^2/b^2=1(a>b>0)的长轴为根号2,离心率 2020-07-30 …
已知点M在椭圆x^2/a^2+y^2/b^2=1(a>b>0)上,以M为圆心的圆与x轴相已知点M在 2020-07-31 …