早教吧作业答案频道 -->数学-->
如图,在正三棱柱ABC-A1B1C1中,已知D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证:(1)直线A1E∥平面ADC1;(2)直线EF⊥平面ADC1.
题目详情
如图,在正三棱柱ABC-A1B1C1中,已知D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证:
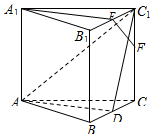
(1)直线A1E∥平面ADC1;
(2)直线EF⊥平面ADC1.

(1)直线A1E∥平面ADC1;
(2)直线EF⊥平面ADC1.
▼优质解答
答案和解析
证明:(1)连接ED,∵D,E分别为BC,B1C1的中点,
∴B1E∥BD且B1E=BD,
∴四边形B1BDE是平行四边形,
∴BB1∥DE且BB1=DE,又BB1∥AA1且BB1=AA1,
∴AA1∥DE且AA1=DE,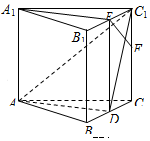
∴四边形AA1ED是平行四边形,
∴A1E∥AD,又∵A1E⊄平面ADC1,AD⊂平面ADC1,
∴直线A1E∥平面ADC1.
(2)在正三棱柱ABC-A1B1C1中,BB1⊥平面ABC,
又AD⊂平面ABC,所以AD⊥BB1,
又△ABC是正三角形,且D为BC的中点,∴AD⊥BC,
又BB1,BC⊂平面B1BCC1,BB1∩BC=B,
∴AD⊥平面B1BCC1,
又EF⊂平面B1BCC1,∴AD⊥EF,
又EF⊥C1D,C1D,AD⊂平面ADC1,C1D∩AD=D,
∴直线EF⊥平面ADC1.
∴B1E∥BD且B1E=BD,
∴四边形B1BDE是平行四边形,
∴BB1∥DE且BB1=DE,又BB1∥AA1且BB1=AA1,
∴AA1∥DE且AA1=DE,

∴四边形AA1ED是平行四边形,
∴A1E∥AD,又∵A1E⊄平面ADC1,AD⊂平面ADC1,
∴直线A1E∥平面ADC1.
(2)在正三棱柱ABC-A1B1C1中,BB1⊥平面ABC,
又AD⊂平面ABC,所以AD⊥BB1,
又△ABC是正三角形,且D为BC的中点,∴AD⊥BC,
又BB1,BC⊂平面B1BCC1,BB1∩BC=B,
∴AD⊥平面B1BCC1,
又EF⊂平面B1BCC1,∴AD⊥EF,
又EF⊥C1D,C1D,AD⊂平面ADC1,C1D∩AD=D,
∴直线EF⊥平面ADC1.
看了 如图,在正三棱柱ABC-A1...的网友还看了以下:
下列包含辩证法思想的是A.水至清则无鱼,人至察则无徒B.得意忘象,得象忘言C.百闻不如一见D.知之 2020-06-07 …
下列项目不属于孔子教育思想的是[]A.兴办”私学B.“温故而知新”C.“仁”的学说D.“知之为知之 2020-07-13 …
孟子云:人不可以无耻。无耻之耻,无耻矣。这句古语告诫我们()A.做人不可以有耻辱感B.不知羞耻,就永 2020-11-03 …
关于苏格拉底名言“美德即知识”的正确理解应当是()A.美德是获得知识的前提B.美德是知识存在的本质所 2020-11-21 …
苏格拉底关注人的伦理道德提出A.天赋人权B.人定胜天C.美德即知识D.知识就是力量 2020-11-25 …
A+、B-、C、D四种微粒中均含有氢原子,且电子总数均为18个.已知溶液中的A+和B-在一定条件下相 2020-12-01 …
下列内容不属于苏格拉底关于道德方面的主张的是[]A.反对过激的民主政治B.道德就是知识C.知识就是道 2020-12-27 …
“知书达理”意为“有文化,懂礼貌”。下列西方名言在内涵上与之最为接近的是()A.“有知识,才有智慧” 2021-01-09 …
以下各项中,属于明朝大儒王阳明提出的思想主张是()A.“己所不欲,勿施于人”B.“天者,理也”C.“ 2021-01-18 …
下列各项不属于孔子的教育思想的有()A.因材施教B.知己知彼,百战不殆C.温故而知新D.知之为知之, 2021-01-20 …