早教吧作业答案频道 -->数学-->
如图所示,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面ABCD是∠ABC=60°的菱形,M为PC的中点,PC=6.(Ⅰ)求证:PC⊥AD;(Ⅱ)求三棱锥M-PAB的体积.
题目详情
如图所示,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面ABCD是∠ABC=60°的菱形,M为PC的中点,PC=
.
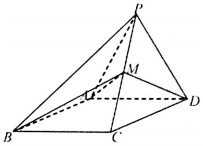
(Ⅰ)求证:PC⊥AD;
(Ⅱ)求三棱锥M-PAB的体积.
| 6 |

(Ⅰ)求证:PC⊥AD;
(Ⅱ)求三棱锥M-PAB的体积.
▼优质解答
答案和解析
证明:(Ⅰ)证法一:连结AC,
由已知得△PAD,△ACD均为正三角形,PA=AC,PD=CD,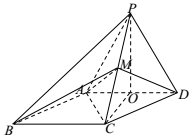
∵M为PC的中点,∴PC⊥AM,PC⊥DM,
又AM,DM⊂平面AMD,AM∩DM=M,
∴PC⊥平面AMD,
又AD⊂平面AMD,∴PC⊥AD.
证法二:取AD的中点O,连结OP,OC,AC,
由已知得△PAD,△ACD均为正三角形,∴OC⊥AD,OP⊥AD,
又OC∩OP=O,OC,OP⊂平面POC,
∴AD⊥平面POC,
又OP⊂平面POC,∴PC⊥AD.
(Ⅱ)∵VM-PAB=
VP-ABC,PO=OC=
,PC=
,
∴PO2+OC2=PC2,∴PO⊥OC,
又OP⊥AD,OC∩AD=O,OC,AD⊂平面ABCD,
∴PO⊥平面ABCD,
又S△ABC=
×2×2×sin60°=
,
∴三棱锥M-PAB的体积VM-PAB=
×
×S△ABC×PO=
×
×
×
=
.
由已知得△PAD,△ACD均为正三角形,PA=AC,PD=CD,

∵M为PC的中点,∴PC⊥AM,PC⊥DM,
又AM,DM⊂平面AMD,AM∩DM=M,
∴PC⊥平面AMD,
又AD⊂平面AMD,∴PC⊥AD.
证法二:取AD的中点O,连结OP,OC,AC,
由已知得△PAD,△ACD均为正三角形,∴OC⊥AD,OP⊥AD,
又OC∩OP=O,OC,OP⊂平面POC,
∴AD⊥平面POC,
又OP⊂平面POC,∴PC⊥AD.
(Ⅱ)∵VM-PAB=
| 1 |
| 2 |
| 3 |
| 6 |
∴PO2+OC2=PC2,∴PO⊥OC,
又OP⊥AD,OC∩AD=O,OC,AD⊂平面ABCD,
∴PO⊥平面ABCD,
又S△ABC=
| 1 |
| 2 |
| 3 |
∴三棱锥M-PAB的体积VM-PAB=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
看了 如图所示,四棱锥P-ABCD...的网友还看了以下:
关于二次根式的﹏设计两个二次根式,经过化简后可表示成a√2的形式(其中a是有理数)的形式,且它们合 2020-04-27 …
已知关于x的二次函数y=ax2和y=bx2.开口大小相同,方向相反,形状相同.求a为什么a=-2呀 2020-05-13 …
6sina²+sinacosa-2cosa²=0,a∈(π/2,π),求sin(2a+π/3)直接 2020-05-14 …
如图所示电场中有A,B两点,则下列说法正确的是如图A-2所示,电场中有A、B两点,则下列说法中正确 2020-05-20 …
求分块矩阵的逆矩阵按我的求法A=(OB)的逆矩镇=A的伴随矩镇/|A|.A的伴随=(0-B).|A 2020-07-09 …
求助高一集合改选并集还是交集?│X+2│+│X-3│<a无空集,求a的范围.解:当x<-2,-x- 2020-07-30 …
设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积是多少?如图,P为三 2020-07-31 …
我们知道对于二次三项式x^2+2ax+a^2这样的完全平方式,可以用公式将它分解成(补充如下)(x 2020-07-31 …
证明不等式a+1-a<a-1-a-2(a≥2)所用的最适合的方法是()A.分析法B.综合法C.反证 2020-08-01 …
关于角与象限对于一个角a,它的半角a/2所在象限可以根据一个图确定,就是把每个象限分成2份,再顺数即 2020-11-20 …