早教吧作业答案频道 -->数学-->
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.(Ⅰ)求证:AE⊥BD';(Ⅱ)求三棱锥A-BCD'的体积.
题目详情
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
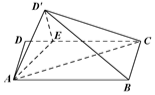
(Ⅰ)求证:AE⊥BD';
(Ⅱ)求三棱锥A-BCD'的体积.

(Ⅰ)求证:AE⊥BD';
(Ⅱ)求三棱锥A-BCD'的体积.
▼优质解答
答案和解析
证明:(Ⅰ)连接BD交AE于点O,依题意得
=
=2,
所以Rt△ABD~Rt△DAE,
所以∠DAE=∠ABD,所以∠AOD=90°,所以AE⊥BD,
即OB⊥AE,OD'⊥AE,又OB∩OD′=O,
OB,OD'⊂平面OBD'.
所以AE⊥平面OBD'.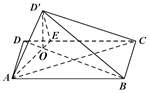
(Ⅱ)因为平面AD'E⊥平面ABCE,
由(Ⅰ)知,OD'⊥平面ABCE,
所以OD'为三棱锥D'-ABC的高,
在矩形ABCD中,AB=4,AD=2,DE=1,所以D′O=
,
所以VA-BCD'=VD'-ABC=
S△ABC•D′O=
×(
×4×2)×
=
即三棱锥A-BCD'的体积为
.
| AB |
| DA |
| AD |
| DE |
所以Rt△ABD~Rt△DAE,
所以∠DAE=∠ABD,所以∠AOD=90°,所以AE⊥BD,
即OB⊥AE,OD'⊥AE,又OB∩OD′=O,
OB,OD'⊂平面OBD'.
所以AE⊥平面OBD'.

(Ⅱ)因为平面AD'E⊥平面ABCE,
由(Ⅰ)知,OD'⊥平面ABCE,
所以OD'为三棱锥D'-ABC的高,
在矩形ABCD中,AB=4,AD=2,DE=1,所以D′O=
| 2 | ||
|
所以VA-BCD'=VD'-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 | ||
|
8
| ||
| 15 |
即三棱锥A-BCD'的体积为
8
| ||
| 15 |
看了 如图,矩形ABCD中,AB=...的网友还看了以下:
一个使我困惑的数学概念,若P、A、B、C为空间不同的四点,且有向量PA=a*向量PB+b*向量PC 2020-05-22 …
河的两岸成平行线,A,B是位于河两岸的两个车间(如图)。要在河上造一座桥,使桥垂直于河岸,并且使A 2020-07-22 …
如果要使a+b>0且ab<0,那么只要()A.a>0且b<0B.a<0且b>0C.a和b异号D.a 2020-07-30 …
定义:对于映射f:A→B,如果A中的不同元素有不同的象,且B中的每一个元素都有原象,则称f:A→B 2020-07-30 …
(1)轩轩想画一个五边形ABCDE,使∠A的度数为奇数,并且使∠B,∠C,∠D,∠E的度数顺次增加 2020-08-01 …
基本不等式的使用问题a+b=1,求(a+2)^2+(b+2)^2的最小值.在这道题里,如果使用基本 2020-08-03 …
有关区间的定义问题让我们回忆实数集合R中区间的精确定义:R的子集E称为一个区间,如果它至少包含两个点 2020-11-20 …
如图所示,一根足够长且不可伸长的细绳通过定滑轮两端系有质量分别为M和m的两个小球A和B,且M=2m. 2020-11-28 …
几个高一集合题集合M包含于集合{1,2,3,4,5}且如果a属于M,则6-a属于M,这样的非空集合M 2020-12-07 …
人体发生酒精过敏时,身体的某些部位(如颈部)出现红肿,原因是细胞释放组织胺,导致毛细血管壁通透性增加 2020-12-17 …