早教吧作业答案频道 -->数学-->
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.(1)求证:平面ABC⊥平面ACD;(2)若E为AB中点,求点A到平面CED的距离.
题目详情
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
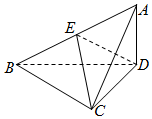
(1)求证:平面ABC⊥平面ACD;
(2)若E为AB中点,求点A到平面CED的距离.

(1)求证:平面ABC⊥平面ACD;
(2)若E为AB中点,求点A到平面CED的距离.
▼优质解答
答案和解析
(1)证明:∵AD⊥平面BCD,BC⊂平面BCD,∴AD⊥BC,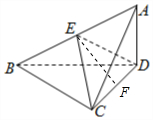
又∵AC⊥BC,AC∩AD=A,∴BC⊥平面ACD,BC⊂平面ABC,
∴平面ABC⊥平面ACD.(6分)
(2) 由已知可得CD=
,取CD中点为F,连接EF,
∵ED=EC=
AB=
,∴△ECD为等腰三角形,
从而EF=
,S△ECD=
,
由(1)知BC⊥平面ACD,∴点E到平面ACD的距离为1,S△ACD=
,
令A到平面CED的距离为d,则VA-ECD=
•S△ECD•d=VE-ACD=
•S△ACD•1,解得d=
.(12分)

又∵AC⊥BC,AC∩AD=A,∴BC⊥平面ACD,BC⊂平面ABC,
∴平面ABC⊥平面ACD.(6分)
(2) 由已知可得CD=
| 3 |
∵ED=EC=
| 1 |
| 2 |
| 2 |
从而EF=
| ||
| 2 |
| ||
| 4 |
由(1)知BC⊥平面ACD,∴点E到平面ACD的距离为1,S△ACD=
| ||
| 2 |
令A到平面CED的距离为d,则VA-ECD=
| 1 |
| 3 |
| 1 |
| 3 |
2
| ||
| 5 |
看了 已知三棱锥A-BCD中,△A...的网友还看了以下:
四面体A-BCD,点A到三边距离相等,则点A在平面BCD内射影是△BCD的内心.这句话对吗为什么 2020-04-26 …
几何题,求证:D,A,E三点共线.在△ABC的BC边上任取一点P,作PD∥AC,PE∥AB,PD、 2020-06-04 …
明明和小亮去敬老院照顾老人7月13日他们去了敬老院他俩约好明明俩天去一次小俩三天去一次.%D%A到 2020-06-06 …
如图,D,E是D,A,E三点所在直线m上的两个动点(D,A,E三点互不相重合),且三角形ABF和三 2020-06-13 …
小学三年级题,李华从A走到B再到c再到D,走了38米.马莉从B走到c再到D再到A,走了31米.这个 2020-06-29 …
如图,从①∠1=∠2②∠C=∠D③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的 2020-07-29 …
如图,汽车从拱形桥顶点A匀速率运动到桥的B点.下列说法正确的是()A.汽车在A点受力平衡B.A到B 2020-08-02 …
扑克牌概率问题在一副52张卡的扑克牌a.抽到大同花顺的概率(10,J,Q,K,A,同一种花式)b.抽 2020-11-07 …
下列各式中正确的是()A.a的二次方=(-a)的二次方B.a的三次方=(-a)的三次方C.a的二次方 2020-11-08 …
如图所示,一带电粒子从A飞到B,径迹如虚线所示,实线为电场线,由此可知()A.粒子带的是正电B.粒子 2020-11-26 …