早教吧作业答案频道 -->数学-->
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为45°,AB和CD是底面圆O上的两条平行的弦,∠COD=60°.(1)证明:平面PAB与平面PCD的交线平行于底面;(2)求轴OP与平面PCD所成的
题目详情
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为45°,AB和CD是底面圆O上的两条平行的弦,∠COD=60°.
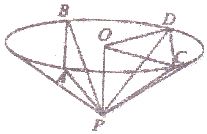
(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求轴OP与平面PCD所成的角的正切值.

(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求轴OP与平面PCD所成的角的正切值.
▼优质解答
答案和解析
(1)证明:设面PAB∩面PCD=直线m,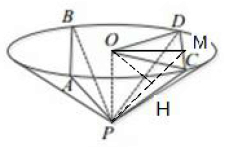
∵AB∥CD,且CD⊂平面PCD,∴AB∥面PCD,得AB∥直线m,
∵AB⊂面ABCD,∴直线m∥面ABCD.
∴面PAB与面PCD的公共交线平行底面ABCD;
(2) 设CD的中点为M,连接OM、PM,
∵OC=OD,∴OM⊥CD,
设OD=r,则OM=
r,
又OP⊥平面OCD,∴OP⊥CD,
又OP∩OM=O,∴CD⊥平面OPM,
过O作OH⊥PM,垂足为H,则CD⊥OH,
又OH∩PM=H,∴OH⊥平面PCD,
∴OP在平面PCD内的射影为PH,
则∠OPH为轴OP与平面PCD所成的角的平面角,
又母线与底面所成的角为45°,即∠ODP=45°,∴OP=OD=r,
在直角△POM中,tan=∠OPM=
,
而∠OPM=∠OPH,∴轴OP与平面PCD所成的角的正切值为
.

∵AB∥CD,且CD⊂平面PCD,∴AB∥面PCD,得AB∥直线m,
∵AB⊂面ABCD,∴直线m∥面ABCD.
∴面PAB与面PCD的公共交线平行底面ABCD;
(2) 设CD的中点为M,连接OM、PM,
∵OC=OD,∴OM⊥CD,
设OD=r,则OM=
| ||
| 2 |
又OP⊥平面OCD,∴OP⊥CD,
又OP∩OM=O,∴CD⊥平面OPM,
过O作OH⊥PM,垂足为H,则CD⊥OH,
又OH∩PM=H,∴OH⊥平面PCD,
∴OP在平面PCD内的射影为PH,
则∠OPH为轴OP与平面PCD所成的角的平面角,
又母线与底面所成的角为45°,即∠ODP=45°,∴OP=OD=r,
在直角△POM中,tan=∠OPM=
| ||
| 2 |
而∠OPM=∠OPH,∴轴OP与平面PCD所成的角的正切值为
| ||
| 2 |
看了 如图,圆锥顶点为P,底面圆心...的网友还看了以下:
把公差d=2的等差数列{an}的各项依次插入等比数列{bn}中将{bn}按原顺序分成1项,2项,4 2020-04-05 …
不同溶度的同种溶液,等质量与等体积混合后质量分数大小的比较?含相同质量的的两种不同溶度的溶液,设等 2020-04-09 …
已知数列{an}是公比为d的等比数列,且a1与a2的算术平均数恰好是a3;(1)求d;(2)设{b 2020-05-13 …
如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针 2020-05-13 …
已知平行四边形ABCD的三个顶点A,B,C的坐标分别为(0,1),(2,1),(-1,3),试求顶 2020-05-13 …
如图是两种昆虫的发育过程.请据图回答:(1)甲图所示的个体发育过程属于.(2)C和D的名称是.在C 2020-05-14 …
已知中心再原点,焦点在x轴上的的椭圆C的焦距为2,离心率为√5/5,设A(5,0),B(1,0)求 2020-05-15 …
哪位好心人帮我回答两道一元一次方程题1.若a,c,d是整数,b是正整数,且满足a+b=c,b+c= 2020-05-21 …
计量数,相对分子质量,物质的质量之间的关系公式例如:已知在2A+B=3C+2D中,A、B、C、D的 2020-05-21 …
数学分析题一道,一百分奖赏一道数学题,数学分析题file:///d:/我的文档/桌面/201012 2020-06-03 …