已知正三棱柱ABC—A1B1C1若过面对角线AB1与另一面对角线BC1平行的平面交上底面A1B1C1的一边A1C1于点D.(1)确定D的位置并证明你的结论;(2)证明平面AB1D⊥平面AA1D;(3)
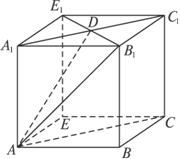
(1)确定D的位置 并证明你的结论;
(2)证明平面AB 1 D⊥平面AA 1 D;
(3)若AB∶AA 1 = 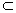 求平面AB 1 D与平面AB 1 A 1 所成角的大小.
求平面AB 1 D与平面AB 1 A 1 所成角的大小.
物体a、b,c叠放在水平桌面上.如图所示,物体A、B和C叠放在水平桌面上,水平力为Fb= 5N,F 2020-05-16 …
已知B1,B2分别是中心在远点,焦点在x轴上椭圆C的上下顶点,F是C的右焦点,FB1=2,F到C的 2020-05-17 …
如图,已知圆O的半径OA=根号5,弦AB=4,点C在弦AB上,以点C为圆心,Co为半径的圆与线段O 2020-05-17 …
如图所示,在光滑的水平面上有两块并列放置的木块A与B,已知A的质量是500g,B的质量是300g, 2020-05-17 …
广场上空有一个气球A,在地面上的B,C两点与点D与点D在一条直线上.广场上空有一个气球A,在地面上 2020-06-17 …
如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点, 2020-07-10 …
如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点, 2020-07-26 …
9.下图是中国历史纪年表(局部),其中的a、b、c、.d指四个朝代。下列说法正确的是()①a是我国封 2020-12-15 …
1.因为上升-2°C与上升2°C的意义相反,所以上升-2°C的意思就是下降2°C,即加上-2就等于减 2020-12-18 …
y=x(X的平方)-4x+3与坐标轴交与A,B,C三点,点P为抛物线上一点,PE垂直于BC与E点,且 2021-01-11 …