早教吧作业答案频道 -->数学-->
(1)如图1,将△ABC纸片沿DE折叠,使点A落在四边形BCDE内点A′的位置,若∠A=40°,求∠1+∠2的度数;(2)通过(1)的计算你发现∠1+∠2与∠A有什么数量关系?请写出这个数量关系,并说
题目详情
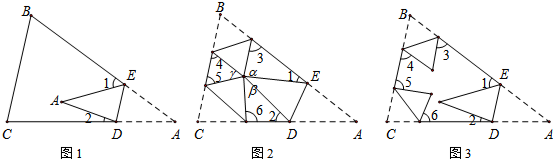
(1)如图1,将△ABC纸片沿DE折叠,使点A落在四边形BCDE内点A′的位置,若∠A=40°,求∠1+∠2的度数;
(2)通过(1)的计算你发现∠1+∠2与∠A有什么数量关系?请写出这个数量关系,并说明这个数量关系的正确性;
(3)将图1中△ABC纸片的三个内角都进行同样的折叠.
①如果折叠后三个顶点A、B、C重合于一点O时,如图2,则图中∠α+∠β+∠γ=___;∠1+∠2+∠3+∠4+∠5+∠6=___;
②如果折叠后三个顶点A、B、C不重合,如图3,则①中的关于“∠1+∠2+∠3+∠4+∠5+∠6”的结论是否仍然成立?请说明你的理由.
(2)通过(1)的计算你发现∠1+∠2与∠A有什么数量关系?请写出这个数量关系,并说明这个数量关系的正确性;
(3)将图1中△ABC纸片的三个内角都进行同样的折叠.
①如果折叠后三个顶点A、B、C重合于一点O时,如图2,则图中∠α+∠β+∠γ=___;∠1+∠2+∠3+∠4+∠5+∠6=___;
②如果折叠后三个顶点A、B、C不重合,如图3,则①中的关于“∠1+∠2+∠3+∠4+∠5+∠6”的结论是否仍然成立?请说明你的理由.

▼优质解答
答案和解析
(1)∵∠A=40°,
∴∠AED+∠ADE=∠A′ED+∠A′DE=140°,
∴∠1+∠2=360°-(∠AED+∠ADE)-(∠A′ED+∠A′DE)=80°,
即∠1+∠2的度数是80°;
(2)∠1+∠2=2∠A,
理由:∵将△ABC纸片沿DE折叠,使点A落在四边形BCDE内点A′的位置,
∴∠AED+∠ADE=∠A′ED+∠A′DE,∠A=∠A′,
∴∠1+∠2
=360°-(∠AED+∠ADE)-(∠A′ED+∠A′DE)
=360°-(180°-∠A)-(180°-∠A′)
=360°-180°+∠A-180°+∠A′
=2∠A,
即∠1+∠2=2∠A;
(3)①由题意可得,∠α+∠β+∠γ=360°-180°=180°,
∠1+∠2+∠3+∠4+∠5+∠6=2∠A+2∠B+2∠C=2(∠A+∠B+∠C)=2×180°=360°,
故答案为:180°,360°;
②如果折叠后三个顶点A、B、C不重合,如图3,则①中的关于“∠1+∠2+∠3+∠4+∠5+∠6”的结论仍然成立;
理由:∵∠1+∠2=2∠A,∠3+∠4=2∠B,∠5+∠6=2∠C,
∴∠1+∠2+∠3+∠4+∠5+∠6
=2∠A+2∠B+2∠C
=2(∠A+∠B+∠C)
=360°,
即如果折叠后三个顶点A、B、C不重合,如图3,则①中的关于“∠1+∠2+∠3+∠4+∠5+∠6”的结论仍然成立.
∴∠AED+∠ADE=∠A′ED+∠A′DE=140°,
∴∠1+∠2=360°-(∠AED+∠ADE)-(∠A′ED+∠A′DE)=80°,
即∠1+∠2的度数是80°;
(2)∠1+∠2=2∠A,
理由:∵将△ABC纸片沿DE折叠,使点A落在四边形BCDE内点A′的位置,
∴∠AED+∠ADE=∠A′ED+∠A′DE,∠A=∠A′,
∴∠1+∠2
=360°-(∠AED+∠ADE)-(∠A′ED+∠A′DE)
=360°-(180°-∠A)-(180°-∠A′)
=360°-180°+∠A-180°+∠A′
=2∠A,
即∠1+∠2=2∠A;
(3)①由题意可得,∠α+∠β+∠γ=360°-180°=180°,
∠1+∠2+∠3+∠4+∠5+∠6=2∠A+2∠B+2∠C=2(∠A+∠B+∠C)=2×180°=360°,
故答案为:180°,360°;
②如果折叠后三个顶点A、B、C不重合,如图3,则①中的关于“∠1+∠2+∠3+∠4+∠5+∠6”的结论仍然成立;
理由:∵∠1+∠2=2∠A,∠3+∠4=2∠B,∠5+∠6=2∠C,
∴∠1+∠2+∠3+∠4+∠5+∠6
=2∠A+2∠B+2∠C
=2(∠A+∠B+∠C)
=360°,
即如果折叠后三个顶点A、B、C不重合,如图3,则①中的关于“∠1+∠2+∠3+∠4+∠5+∠6”的结论仍然成立.
看了 (1)如图1,将△ABC纸片...的网友还看了以下:
填写与人体及人体器官或部位有关的成语 2020-03-30 …
2016年10月,中央纪委宣传部、中央电视台联合制作的八集专题片《永远在路上》播出,8集、400分 2020-04-07 …
填字组成语!如题填动物名称:()头小楷、()程万里.填表示颜色词语:()男绿女、()田生玉、半() 2020-04-27 …
怎么判断LG水位开关好坏?我的洗衣机水停不了,但是把气管拔开用嘴巴吹气水可以停.感觉不到水位开关哪 2020-05-16 …
填与人体器官、部位有关的成语\(^o^)/~( )来( )去 ( )亡( )寒 ( )濡( )染 2020-05-17 …
下面与嵌入式处理器复位相关的叙述中,错误的是()。A.嵌入式处理器都有一个系统复位引脚为nRESET 2020-05-23 …
高低压压力控制器中的手动复位开关的作用是( )。A.手动复位后使机组启动控制电路接通B.手动复位后 2020-06-07 …
谁知道与身体部位有关的英语短语? 2020-06-23 …
请在成语后面天上一位有关的历史人物投笔从戒约法三章完壁归赵闻鸡起舞百步穿杨慷慨悲歌负荆请罪洛阳纸贵 2020-07-10 …
本单元出现了和身体部位有关的病痛类的名词,请同学们注意:身体部位有的是单数,如:鼻子nose嘴巴m 2020-07-27 …