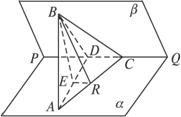
如图已知二面角α-PQ-β为60°点A和点B分别在平面α和平面β内点C在棱PQ上∠ACP=∠BCP=30°CA=CB=a.(1)求证:AB⊥PQ;(2)求点B到平面α的距离;(3)设R是线段CA上的一点直线BR与平面α所成

Question

如图 已知二面角α-PQ-β为60° 点A和点B分别在平面α和平面β内 点C在棱PQ上 ∠ACP=∠BCP=30° CA=CB=a.

(1)求证:AB⊥PQ;

(2)求点B到平面α的距离;

(3)设R是线段CA上的一点 直线BR与平面α所成的角为45° 求线段CR的长度.

Answer 1

(1)证明:在平面β内作BD⊥PQ于D 连结AD.

    ∵∠ACP=∠BCP=30° CA=CB=a CD公用

    ∴△ACD≌△BCD.

    ∴∠ADC=∠BDC=90° 即AD⊥PQ.

    于是PQ⊥平面ABD 则AB⊥PQ.

(2)解:由(1)知∠ADB是二面角α-PQ-β的平面角

    ∴∠ADB=60°.又PQ⊥平面ABD

    ∴α⊥平面ABD.

    过B作BE⊥AD于点E 则BE即为B到平面α的距离.

    BE=BD·sin60°=BC·sin30°·sin60°= a.

 (3)解:连结ER

    ∵BE⊥α

    ∴∠BRE是BR与α所成的角

    即∠BRE=45° 则有BR= = a.

    易知△ABD为正三角形 AB=AD=BD= a.

    在△ABC中 由余弦定理得cos∠BCA= .

    在△BCR中 设CR=x 由余弦定理得( a) ² =x ² +a ² -2ax· 求得x ₁ = x ₂ = (舍去 ∵CR＜AC=a) 故CR= .