如图，射线OC，与x轴的夹角为30o，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线y=x2（x>0）上取点P，在y轴上取点Q，使得以P、O、Q为顶点的三角形与△AOH全等，则符合条件的点A的个数

Question

如图，射线OC，与x轴的夹角为30^o，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线y=x²（x>0）上取点P，在y轴上取点Q，使得以P、O、Q为顶点的三角形与△AOH全等，则符合条件的点A的个数是（　　）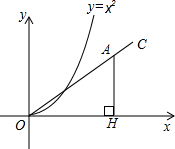

A. 1

B. 2

C. 3

D. 4

Answer 1

①当∠POQ=∠OAH=60°时，此时A、P重合，可联立直线OA和抛物线的解析式，即可得A点坐标；
②当∠POQ=∠AOH=30°时，此时∠POH=60°，即直线OP：y=√(3)x，
联立抛物线的解析式可得P点坐标，进而可求出OQ、PQ的长，由于△POQ≌△AOH，那么OH=OQ、AH=PQ，由此得到点A的坐标；
③当∠OPQ=90°时，∠POQ=∠AOH=30°时，此时△QOP≌△AOH；
④当∠OPQ=90°时，∠POQ=∠OAH=60°，此时△OQP≌△AOH；
综上可知满足条件的A点有4个，
故选D．