早教吧作业答案频道 -->数学-->
如图,抛物线y=ax2-32x-2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值
题目详情
如图,抛物线y=ax2-
x-2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
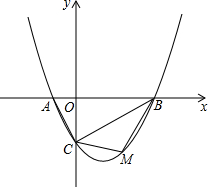
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
| 3 |
| 2 |

(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
▼优质解答
答案和解析
(1)将B(4,0)代入抛物线的解析式中,得:
0=16a-
×4-2,即:a=
;
∴抛物线的解析式为:y=
x2-
x-2.
(2)可得:B(4,0)、C(0,-2),设直线BC的解析式为:y=kx+b,
则
,
解得:
故直线BC的解析式为:y=x-2;
设xM=t,则yM=
t2-
t-2,yN=
t-2,
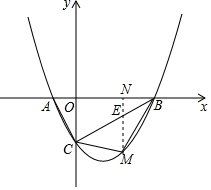
S△MBC=S△CME+S△BEM=
EM•ON+
EM•BN=
EM•OB
=
(
t-2-
t2+
t+2)×4
=-t2+4t
=-(t-2)2+4,
∴当t=2时,S△MBC=最大值为4,此时M(2,-3);
(3)由(1)的函数解析式可求得:A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(1.5,0).
0=16a-
| 3 |
| 2 |
| 1 |
| 2 |

∴抛物线的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)可得:B(4,0)、C(0,-2),设直线BC的解析式为:y=kx+b,
则
|
解得:
|
故直线BC的解析式为:y=x-2;
设xM=t,则yM=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
S△MBC=S△CME+S△BEM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=-t2+4t
=-(t-2)2+4,
∴当t=2时,S△MBC=最大值为4,此时M(2,-3);
(3)由(1)的函数解析式可求得:A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(1.5,0).
看了 如图,抛物线y=ax2-32...的网友还看了以下:
下列选项体现具体问题具体分析的是[]A.张冠李戴、良莠不分B.统筹兼顾、适当安排C.因材施教、量体 2020-05-16 …
A,B两点到平面α的距离分别是3cm,5cm,点M是A,B的中点,则点M到平面α的距离是多少? 2020-05-16 …
读岩石圈板块分布地球剖面示意图(局部),完成28、29题。28.宏观地形M是A.巨大裂谷B.低缓高 2020-05-16 …
以下各种情况中可能引起混凝土离析的是( )A.混凝土自由下落高度为3m B.混凝土温度过高C.振捣时 2020-05-18 …
设M={x∣x²+x+2=0,x∈R},a=lg(lg10),则{a}与M的关系是M是{a}的真子 2020-05-22 …
loga^mb^n=?是n/mlogab还是logn/maba是底数m是a的指数b是真数n是b的指 2020-05-22 …
业务分析是系统分析的一项重要内容,不属于业务分析的是( )A.绘制企业的组织结构图B.绘制企业的业 2020-05-23 …
可行性分析包括经济、技术和运行的可行性分析,属于运行可行性分析的是( )A.投资的必要性B.技术人 2020-05-23 …
已知函数y=f(x)在R上为奇函数,且当x≥0时,f(x)=x^2-2x,则f(x)在x≤0时的解 2020-06-06 …
读岩石圈板块分布地球剖面示意图(局部),完成18-19题。18.宏观地形M是A.巨大裂谷B.低缓高 2020-06-26 …