早教吧作业答案频道 -->数学-->
设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于任何一个二次函数,它在给定的闭区间上都有最小值.(1)函数y=-x2+4x-2
题目详情
设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于任何一个二次函数,它在给定的闭区间上都有最小值.
(1)函数y=-x2+4x-2在区间[0,5]上的最小值是___
(2)求函数y=(x+
)2+
在区间[0,
]上的最小值.
(3)求函数y=x2-4x-4在区间[t-2,t-1](t为任意实数)上的最小值ymin的解析式.
(1)函数y=-x2+4x-2在区间[0,5]上的最小值是___
(2)求函数y=(x+
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
(3)求函数y=x2-4x-4在区间[t-2,t-1](t为任意实数)上的最小值ymin的解析式.
▼优质解答
答案和解析
(1)y=-x2+4x-2其对称轴为直线为x=2,顶点坐标为(2,2),函数图象开口向下.
函数图大致象如图1所示:
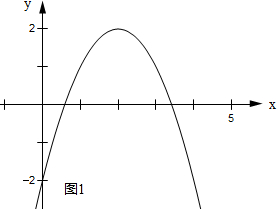
当x=5时,函数有最小值,最小值为-7.
故答案为:-7.
(2)y=(x+
)2+
,其对称轴为直线x=-
,顶点坐标(-
,
),且图象开口向上.
其顶点横坐标不在区间[0,
]内,
如图2所示.
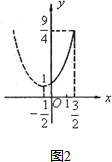
当x=0时,函数y有最小值
=1.
(3)将二次函数配方得:y=x2-4x-4=(x-2)2-8
其对称轴为直线:x=2,顶点坐标为(2,-8),图象开口向上
若顶点横坐标在区间[t-2,t-1]左侧,则2<t-2,即t>4.
当x=t-2时,函数取得最小值:ymin=(t-4)2-8=t2-8t+8
若顶点横坐标在区间[t-2,t-1]上,则t-2≤2≤t-1,即3≤t≤4.
当x=2时,函数取得最小值:ymin=-8
若顶点横坐标在区间[t-2,t-1]右侧,则t-1<2,即t<3.
当x=t-1时,函数取得最小值:ymin=(t-3)2-8=t2-6t+1
综上讨论,得ymin=
.
函数图大致象如图1所示:

当x=5时,函数有最小值,最小值为-7.
故答案为:-7.
(2)y=(x+
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
其顶点横坐标不在区间[0,
| 3 |
| 2 |
如图2所示.

当x=0时,函数y有最小值
| y | min |
(3)将二次函数配方得:y=x2-4x-4=(x-2)2-8
其对称轴为直线:x=2,顶点坐标为(2,-8),图象开口向上
若顶点横坐标在区间[t-2,t-1]左侧,则2<t-2,即t>4.
当x=t-2时,函数取得最小值:ymin=(t-4)2-8=t2-8t+8
若顶点横坐标在区间[t-2,t-1]上,则t-2≤2≤t-1,即3≤t≤4.
当x=2时,函数取得最小值:ymin=-8
若顶点横坐标在区间[t-2,t-1]右侧,则t-1<2,即t<3.
当x=t-1时,函数取得最小值:ymin=(t-3)2-8=t2-6t+1
综上讨论,得ymin=
|
看了 设a,b是任意两个不等实数,...的网友还看了以下:
这些根人体有关心脏部位他们各表示什么?如:手腕比喻手段;手足比喻兄弟;手头比喻钱的多少等。那么下列 2020-05-12 …
小明设计的一个气体温度计的示意图.瓶中装的是气体,瓶塞不漏气,横管中间有一段小液柱.小明通过实验发 2020-05-20 …
如图所示,有1、2、3三个质量均为m=1kg的物体,物体2与物体3通过不可伸长轻绳连接,跨过光滑的 2020-06-11 …
如图所示,有一水平放置的足够长的皮带输送机以v=5m/s的速率沿顺时针方向运行.有一物体以v0=1 2020-06-20 …
西航小学体育器材室里的足球个数十排球的2倍,体育活动课上,每班借7个足球,5个排球,排球接完时,足 2020-06-27 …
(2014•泰安)钙是维持维持人体正常功能所必需的元素,有时需要服用补钙剂满足人体需求.如图分别为 2020-06-29 …
某校体育里的足球个数是排球的3倍.体育活动课上,每班肯借六个足球和五个排球,排球借完时,还有72个 2020-06-30 …
某体育室里的足球个数是排球个数的3倍,每班借3个足球,4个排球,排球借完时体育室内还有63个足球.体 2020-10-30 …
如图所示,有一与水平面成θ角的传送带AB,长度为L,以恒定速率v向上传送,现在A端放上质量为m的物体 2020-12-09 …
肾气不足身体有炎症导致先天性雀斑怎么治疗 2021-06-07 …