早教吧作业答案频道 -->数学-->
正△ABC的边长为2,M是AB边上的中点,P是BC边上的任意一点,PA+PM的最大值是,最小值是.
题目详情
正△ABC的边长为2,M是AB边上的中点,P是BC边上的任意一点,PA+PM的最大值是___,最小值是___.
▼优质解答
答案和解析
如图1所示:作点M关于CB的对称点M′连接AM′、M′C.
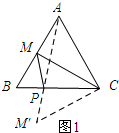
∵点M与点M′关于BC对称,
∴MP=M′P,∠MCP=∠M′CP.
∵△ABC是正三角形,M是AB的中点,
∴MC=CM′,∠MCP=∠ACP=30°.
∴∠MCP=∠ACP=∠M′CP=30°.
∴CM′=MC=BC×cos30°=2×
=
.
∴∠ACM′=90°.
∴AM′=
=
.
∴PA+PM的最小值是
.
如图2所示:当点P与点C重合时.PM+PA有最大值.
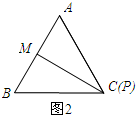
∵PM=
,AP=2,
∴PA+PM=2+
.
故答案为:2+
;
.

∵点M与点M′关于BC对称,
∴MP=M′P,∠MCP=∠M′CP.
∵△ABC是正三角形,M是AB的中点,
∴MC=CM′,∠MCP=∠ACP=30°.
∴∠MCP=∠ACP=∠M′CP=30°.
∴CM′=MC=BC×cos30°=2×
| ||
| 2 |
| 3 |
∴∠ACM′=90°.
∴AM′=
| AM2+M′C2 |
| 7 |
∴PA+PM的最小值是
| 7 |
如图2所示:当点P与点C重合时.PM+PA有最大值.

∵PM=
| 3 |
∴PA+PM=2+
| 3 |
故答案为:2+
| 3 |
| 7 |
看了 正△ABC的边长为2,M是A...的网友还看了以下:
如图所示的电路中,a、b、c三只小灯泡均发光,当把变阻器R的滑动片P向下滑动时,三只灯泡的明暗变化 2020-04-08 …
如图物体A、B、C叠放在水平桌面上,水平力F作用于C物体,使A、B、C以共同速度向右匀速运动,关于 2020-05-13 …
对于平衡体系:A+B(s)C,增大压强,B的转化率增大,则A和C的状态应是()A.A为固体、C为固 2020-05-14 …
下面哪一组命题公式不是等值的?()A.┐(A→B),A∧┐BB.┐(A←→B),(A∧┐B)∨(┐ 2020-05-17 …
下面哪一组命题公式不是等值的?()A.(AB),A∧BB.(AB),(A∧B)∨(A 2020-05-17 …
下面哪一组命题公式不是等值的?()A.┐(A→B),A∧┐BB.┐(A←→B),(A∧┐B)∨(┐ 2020-05-17 …
c÷d=1,a×b=1.根据这两个式子可以确定()A.c是倒数B.d是倒数C.a是倒数D.a和b互 2020-06-15 …
下列不符合如图关系的是()A.a是有细胞壁的生物、b是植物、c是发菜B.a是细胞核、b是染色质、c 2020-06-19 …
如图所示,若悬绳A和弹簧秤B的重力不计,下列各对力中属于平衡力的是()A.A对B的拉力与B对C的拉 2020-06-26 …
如图表示在某生态系统中,a、b、c三个种群数量变化相互关系,下列描述正确的是()A.a肯定是生产者 2020-06-26 …