早教吧作业答案频道 -->数学-->
如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.(1)求证:∠ECD=∠EDC;(2)若tanA=14,求DE长;(3)当∠A从1
题目详情
如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
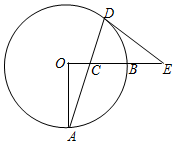
(1)求证:∠ECD=∠EDC;
(2)若tanA=
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.

(1)求证:∠ECD=∠EDC;
(2)若tanA=
| 1 |
| 4 |
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
▼优质解答
答案和解析
 (1)证明:连结OD,
(1)证明:连结OD,
∵DE是⊙O的切线,
∴∠EDC+∠ODA=90°,
∵OA⊥OB,
∴∠ACO+∠A=90°,
∵OA=OD,
∴∠ODA=∠A,
∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,
∴∠ECD=∠EDC.
(2) ∵tanA=
,
∴
=
,
∴OC=2,
设DE=x,
∵∠ECD=∠EDC,
∴CE=x,
∴OE=2+x.
∴∠ODE=90°,
∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,
∴DE=CE=15.
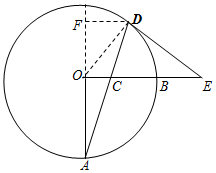
(3) 过点D作AO的垂线,交AO的延长于F,
当∠A=15°时,∠DOF=30°,DF=4,
S弓形ABD=
-
×8×4=
-16
当∠A=30°时,∠DOF=60°,DF=4
,
S弓形ABD=
-
×8×4
=
-16
,
∴S=(
-16)-(
-16
)=
π+16
-16
 (1)证明:连结OD,
(1)证明:连结OD,∵DE是⊙O的切线,
∴∠EDC+∠ODA=90°,
∵OA⊥OB,
∴∠ACO+∠A=90°,
∵OA=OD,
∴∠ODA=∠A,
∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,
∴∠ECD=∠EDC.
(2) ∵tanA=
| OC |
| OA |
∴
| OC |
| 8 |
| 1 |
| 4 |
∴OC=2,
设DE=x,
∵∠ECD=∠EDC,
∴CE=x,
∴OE=2+x.
∴∠ODE=90°,
∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,
∴DE=CE=15.
(3) 过点D作AO的垂线,交AO的延长于F,
当∠A=15°时,∠DOF=30°,DF=4,
S弓形ABD=
| 150π•64 |
| 360 |
| 1 |
| 2 |
| 80π |
| 3 |
当∠A=30°时,∠DOF=60°,DF=4
| 3 |
S弓形ABD=
| 120π•64 |
| 360 |
| 1 |
| 2 |
| 3 |
| 64π |
| 3 |
| 3 |
∴S=(
| 80π |
| 3 |
| 64π |
| 3 |
| 3 |
| 16 |
| 3 |
| 3 |
看了 如图,OA,OB是⊙O的两条...的网友还看了以下:
∑(2^n)/(n^n)的收敛性你回答的是:取后一项后前一项的比.(2^n+1)/((n+1)^(n 2020-03-31 …
如何化简C中的所有项,使得他们保留5位有效数字?%随机生成一个多项式作为测试用例symsnf=sum 2020-03-31 …
对{a(n)},括号里的n是下标,有a(n)^2-ba(n)=a(n-1)^2,n>=2,b>0, 2020-04-27 …
(m十1)x的立方y一(n一4)xx的平方y的n一l次方十5xy一1是四次三项式 2020-05-12 …
已知函数f(x)=((4*2^x)+2)/((2^x)+1)+xcosx(-1≤x≤1),且f(x 2020-05-13 …
有一些自然数n,满足:2n - n 是3的倍数,3n - n 是5的倍数,5n - n是2的倍数. 2020-05-16 …
数列{an}的n是非零自然数,数列{a(2n+1)}的n一定是自然数吗 这两个数列为什么不同 2020-05-16 …
若n(n∈N,n>1)不能被小于根号n的所有质数整除,则n为质数.谁证明下.这次有分加了...括号 2020-05-17 …
证明:当0<b<a,且n>1时,有n(a-b)b^(n一1)<(a^n-b^n)<n(a一b)a^ 2020-05-19 …
在平面直角坐标系中,已知An(n,an)、Bn(n,bn)、Cn(n-1,0)(n∈N*),满足向 2020-05-22 …