早教吧作业答案频道 -->数学-->
如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R(1)设BP=x,DQ=y,求y与x的函数解析式,并写出定义域;(2)求∠PRQ的
题目详情
如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R
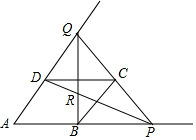
(1)设BP=x,DQ=y,求y与x的函数解析式,并写出定义域;
(2)求∠PRQ的度数.

(1)设BP=x,DQ=y,求y与x的函数解析式,并写出定义域;
(2)求∠PRQ的度数.
▼优质解答
答案和解析
(1)∵四边形ABCD是边长为a的菱形,∠A=60°,
∴CD=BC=a,AD∥BC,∠ADC=∠ABC=120°,
∴∠DQC=∠BCP,∠QDC=∠CBP=60°,
∴△QDC∽△PBC,
∴
=
,
即
=
,
∴y=
(x>0);
(2)连接BD,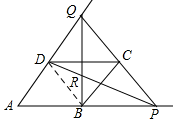
∵四边形ABCD是边长为a的菱形,且∠A=60°,
∴∠ABC=∠ADC=120°,∠ADB=∠ABD=60°,BD=AB=a,
∴∠QDB=180°-∠ADB=120°,∠DBP=180°-∠ABD=120°,
∴∠QDB=∠DBP,
又∵
=
=
=
,
=
,
∴
=
,
∴∠QDB∽△DBP,
∴∠BDP=∠DQB,
∵∠PRQ是△QDR的外角,
∴∠PRQ=∠DQB+∠QDR=∠BDP+∠QDR=∠BDQ=120.
∴CD=BC=a,AD∥BC,∠ADC=∠ABC=120°,
∴∠DQC=∠BCP,∠QDC=∠CBP=60°,
∴△QDC∽△PBC,
∴
| DQ |
| BC |
| CD |
| PB |
即
| y |
| a |
| a |
| x |
∴y=
| a2 |
| x |
(2)连接BD,

∵四边形ABCD是边长为a的菱形,且∠A=60°,
∴∠ABC=∠ADC=120°,∠ADB=∠ABD=60°,BD=AB=a,
∴∠QDB=180°-∠ADB=120°,∠DBP=180°-∠ABD=120°,
∴∠QDB=∠DBP,
又∵
| QD |
| BD |
| y |
| a |
| ||
| a |
| a |
| x |
| BD |
| PB |
| a |
| x |
∴
| QD |
| BD |
| BD |
| PB |
∴∠QDB∽△DBP,
∴∠BDP=∠DQB,
∵∠PRQ是△QDR的外角,
∴∠PRQ=∠DQB+∠QDR=∠BDP+∠QDR=∠BDQ=120.
看了 如图,四边形ABCD是边长为...的网友还看了以下:
设a,b是一个直角三角形两条直角边的长,且(a的平方+b的平方)(a的平方+b的平方+4)=21, 2020-04-27 …
设a、b、c是直角三角形的三边,c为斜边,n为正整数,试判断an+bn与cn的关系,并证明你的结论 2020-05-14 …
设a表示一个两位数,b是一个3位数,现在把a放在b的左边,组成一个五位数为X,再把b放在a的左边, 2020-05-19 …
设|a|=4,|b|=3,向量a,b夹角是30度,求以a+2b和a-3b为边的平行四边形的面积是? 2020-06-06 …
如图,在平面直角坐标系的第一象限上,反比例函数y=a/x(x>0)的图像与矩形OABC的两条边相交 2020-06-06 …
设a,b,c是素数,记x=b+c-a,y=c+a-b,z=a+b-c,当z2=y,x−y=2时,a 2020-06-12 …
已知:如图,在△ABC中,∠C=90°,AC=BC=4,点M是边AC上一动点(与点A、C不重合), 2020-07-17 …
对下列实验设计操作中,所观察到的实验现象描述和所得结论一定正确的是()实验现象结论A左边烧杯中铁表面 2020-12-23 …
a+=a-=a+a假设a=9,书上结果是-18但是a-=18,不是应该先把a赋18-18吗,如果不是 2020-12-31 …
设△三边上的三个内接正方形(两个顶点在三角形的一边上,其余两个顶点分别在三角形的另两边上)的面积相等 2021-02-04 …