早教吧作业答案频道 -->数学-->
△ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b-2bcosA.(1)求bc的值;(2)设AB的中垂线交BC于D,若cos∠ADC=1732,b=2,求△ABC的面积.
题目详情
△ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b-2bcosA.
(1)求
的值;
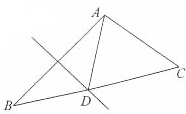
(2)设AB的中垂线交BC于D,若cos∠ADC=
,b=2,求△ABC的面积.

(1)求
| b |
| c |
(2)设AB的中垂线交BC于D,若cos∠ADC=
| 17 |
| 32 |
▼优质解答
答案和解析
(1)∵2acosB=3b-2bcosA,
∴2sinAcosB=3sinB-2sinBcosA
∴2sin(A+B)=3sinB,则2sinC=3sinB,
由正弦定理得,
=
=
;
(2)∵AB的中垂线交BC于D,∴DA=DB,则∠B=∠BAD,
∴∠ADC=∠B+∠BAD=2∠B,
∵cos∠ADC=
,∴cos∠ADC=1-2sin2B=
,
解得sinB=
,
由B是锐角得,cosB=
=
,
∵在△ABC中,b=2,且
=
,∴c=3,
由余弦定理得,b2=a2+c2-2accosB,
∴4=a2+9-2×3×a×
,解得a=4或
,
∵BD=
=
>
,∴a=
舍去,
∴△ABC的面积S=
acsinB=
×4×3×
=
.
∴2sinAcosB=3sinB-2sinBcosA
∴2sin(A+B)=3sinB,则2sinC=3sinB,
由正弦定理得,
| b |
| c |
| sinB |
| sinC |
| 2 |
| 3 |
(2)∵AB的中垂线交BC于D,∴DA=DB,则∠B=∠BAD,
∴∠ADC=∠B+∠BAD=2∠B,
∵cos∠ADC=
| 17 |
| 32 |
| 17 |
| 32 |
解得sinB=
| ||
| 8 |
由B是锐角得,cosB=
| 1-sin2B |
| 7 |
| 8 |
∵在△ABC中,b=2,且
| b |
| c |
| 2 |
| 3 |
由余弦定理得,b2=a2+c2-2accosB,
∴4=a2+9-2×3×a×
| 7 |
| 8 |
| 5 |
| 4 |
∵BD=
| ||
| cosB |
| 12 |
| 7 |
| 5 |
| 4 |
| 5 |
| 4 |
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 8 |
3
| ||
| 4 |
看了 △ABC中,角A、B、C所对...的网友还看了以下:
谁能给我讲下余玄定理,推导和应用,,有c=a-b,c^2=(a-b)·(a-b)=a^2+b^2-2 2020-03-31 …
矢量a×b×c=a×(b×c)=(a×b)×c=么?a×(b×c)=(ac)b-(ab)ca×b× 2020-04-05 …
分解因式a(a-b-c)+b(c-a+b)+c(b-a+c)的结果是()A.(b+c-a)2B.( 2020-04-08 …
为什么[(a+b)^2-c^2)][(a-b)^2-c^2)]=(a+b+c)(a+b-c)(a- 2020-04-26 …
如何确定偏导数极值?例如:已知a,b,c是满足a^2=b^2+c^2的正数,求函数f(a,b,c) 2020-04-26 …
将下列式子写成(A+B)(A-B)的形式①(-a+b+c-d)(-a-b+c+d)②(a+b将下列 2020-04-27 …
matlab解中学三角函数方程数学题,不会求大大~~~~~~~~~~[a,b,c,A,B,C]=s 2020-05-14 …
公务员假言命题逻辑:如果A评优了,那么B和C也能评优.为什么是"A→B且C"而不是"A→B或C"公 2020-05-16 …
a,b,c,都为非零自然数,若a÷c/b>a,则() A,b>c B,a>c C,b>c 2020-05-16 …
下面哪一组命题公式不是等值的?()A.┐(A→B),A∧┐BB.┐(A←→B),(A∧┐B)∨(┐ 2020-05-17 …