早教吧作业答案频道 -->数学-->
(1)如图①,在Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,交BC于点D.如果作辅助线DE⊥AB于点E,则可以得到AC、CD、AB三条线段之间的数量关系为;(2)如图,△ABC中,∠C=2∠B,AD平
题目详情
(1)如图①,在Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,交BC于点D.如果作辅助线DE⊥AB于点E,则可以得到AC、CD、AB三条线段之间的数量关系为___;
(2)如图,△ABC中,∠C=2∠B,AD平分∠BAC,交BC于点D.(1)中的结论是否仍然成立?若不成立,试说明理由;若成立,请证明.
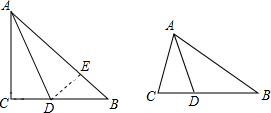
(2)如图,△ABC中,∠C=2∠B,AD平分∠BAC,交BC于点D.(1)中的结论是否仍然成立?若不成立,试说明理由;若成立,请证明.

▼优质解答
答案和解析
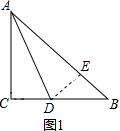 (1)如图1,∵AD平分∠BAC,
(1)如图1,∵AD平分∠BAC,
∴∠CAD=∠EAD,
在△CAD和△EAD中
,
∴△CAD≌△EAD(AAS),
∴CD=DE,AC=AE,
∵∠B=45°,∠DEB=90°,
∴DE=EB,
∴DC=BE,
∴AE+BE=AC+DC=AB;
故答案为:AB=AC+CD.
(2)成立.
证明:如图2,在AB上截取AE=AC,连接DE.
∵在△ACD和△AED中
,
∴△ACD≌△AED(SAS),
∴CD=ED,∠C=∠AED,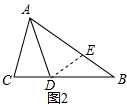
又∵∠C=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴2∠B=∠B+∠EDB,
∴∠B=∠EDB,
∴ED=EB
∵AB=AE+EB,ED=EB=CD,AE=AC,
∴AB=AC+CD.
 (1)如图1,∵AD平分∠BAC,
(1)如图1,∵AD平分∠BAC,∴∠CAD=∠EAD,
在△CAD和△EAD中
|
∴△CAD≌△EAD(AAS),
∴CD=DE,AC=AE,
∵∠B=45°,∠DEB=90°,
∴DE=EB,
∴DC=BE,
∴AE+BE=AC+DC=AB;
故答案为:AB=AC+CD.
(2)成立.
证明:如图2,在AB上截取AE=AC,连接DE.
∵在△ACD和△AED中
|
∴△ACD≌△AED(SAS),
∴CD=ED,∠C=∠AED,

又∵∠C=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴2∠B=∠B+∠EDB,
∴∠B=∠EDB,
∴ED=EB
∵AB=AE+EB,ED=EB=CD,AE=AC,
∴AB=AC+CD.
看了 (1)如图①,在Rt△ABC...的网友还看了以下:
如图,点2位于点3的什么位置?这里是用上北下南作戏右东的方法判断吗?可以根据经纬线判断吗?怎么判断 2020-05-16 …
1点3x 减3点2等于13点7解方程过程写全跪求 2020-05-16 …
在梯形ABCD中角B=45度角C=30度上底AD=1下底BC=9求梯形面积只要求出高就行要用辅助线 2020-05-23 …
(2)关于计算机辅助技术的描述中,正确的是( )。A)计算机辅助设计缩写为CAS B)计算机辅助制造 2020-05-23 …
已知甲地(32°N,120°E)和乙地为对趾点。据此回答下列各题。1.与乙地最靠近的地点是图中的( 2020-07-06 …
英语翻译1.昨晚刮了一场大风,今天的温度将会下降一点.2.由于大雾,火车没有按时到站.3.今天的天 2020-07-14 …
数学解方程5X减4点5乘5等于5点5.X等于多少.2X除0点6等于4点5.X等于多少.6X减1点2 2020-07-17 …
英语翻译1.导入大量数据时,因为服务器有运行时间的限制,超过它的时间就有可能后面有一些数据无法导入. 2020-11-03 …
(1/2)关于一篇周末该不该参加辅导班或请家教的英语作文!内容:优点:补习薄弱功课,提前预习新课,. 2020-11-28 …
有一个偏心轮绕O点匀角速转动,O点不在圆心,O点在圆内,试找出偏心轮上:1位于轮缘线速度最大的点2位 2021-01-02 …