（12分）圆、椭圆、双曲线都有对称中心，统称为有心圆锥曲线，它们统一的标准方程为.圆的很多优美性质可以类比推广到有心圆锥曲线中如圆的“垂径定理”的逆定理:

Question

（ 12 分）圆、椭圆、双曲线都有对称中心，统称为有心圆锥曲线，它们统一的标准方程为 . 圆的很多优美性质可以类比推广到有心圆锥曲线中 如圆的“垂径定理”的逆定理 : 圆的平分弦（不是直径）的直径垂直于弦 . 类比推广到有心圆锥曲线： 已知直线 与曲线 ： 交于 两点， 的中点为 ，若直线 和 ( 为坐标原点 ) 的斜率都存在，则 . 这个性质称为 有心圆锥曲线的“垂径定理” .

（Ⅰ）证明 有心圆锥曲线的“垂径定理” ；

（Ⅱ）利用 有心圆锥曲线的“垂径定理”解答下列问题：

①      过点 作直线 与椭圆 交于 两点，求 的中点 的轨迹 的方程；

②      过点 作直线 与 有心圆锥 曲线 交于 两点，是否存在这样的直线 使点 为 线段 的中点？ 若存在，求直线 的方程；若不存在，说明理由 .

Answer 1

解析： （Ⅰ）证明 设

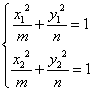
相减得   

注意到   

有         

即                          ………………………………………… 5 分

（Ⅱ）①设

由垂径定理，

即        

化简得   

当 与 轴平行时， 的坐标也满足方程 .

故所求 的中点 的轨迹 的方程为 ；

………………………………………… 8 分

②      假设过点 P(1 1) 作直线 与 有心圆锥 曲线 交于 两点，且 P 为 的中点，则

         

由于  

直线 ，即 ， 代入曲线 的方程得

          即   

         由   得 .

故当 时，存在这样的直线，其直线方程为 ；

当 时，这样的直线不存在 .         ……………………………… 12 分