早教吧作业答案频道 -->数学-->
如图,边长为6的正方形ABCD中,点E是BC上一点,点F是AB上一点.点F关于直线DE的对称点G恰好在BC延长线上,FG交DE于点H.点M为AD的中点,若MH=17,则EG=.
题目详情
如图,边长为6的正方形ABCD中,点E是BC上一点,点F是AB上一点.点F关于直线DE的对称点G恰好在BC延长线上,FG交DE于点H.点M为AD的中点,若MH=
,则EG=___.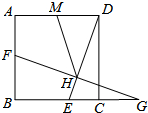
| | 17 |

▼优质解答
答案和解析
连接DF,DG,过H作HP⊥AB于P,HQ⊥AD于Q,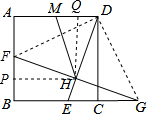
∵点F,点G关于直线DE的对称,
∴DF=DG,
正方形ABCD中,∵AD=CD,∠ADC=∠A=∠BCD=90°,
∴∠GCD=90°,又在Rt△AFD与Rt△CDG中,
,
∴Rt△AFD≌Rt△CDG,
∴∠ADF=∠CDG,
∴∠FDG=∠ADC=90°,
∴△FDG是等腰直角三角形,
∵DH⊥CF,
∴DH=FH=
FG,
∵HP⊥AB,HQ⊥AD,∠A=90°,
∴四边形APHQ是矩形,
∴∠PHQ=90°,
∵∠DHF=90°,
∴∠PHF=∠DHQ,又在△PFF与△DQH中有
,
∴△HPF≌△DHQ,
∴HP=HQ,所以矩形APHQ是正方形;
设正方形APHQ边长为a,则在Rt△MQH中,有(a-3)2+a2=17,解得a=4;
∴FP=QD=AD-AQ=6-4=2,
又易证△FPH∽△EHG,则有
=
,即EG=
,
又FH2=22+42=20,PH=4,
∴EG=5
故答案为:5.

∵点F,点G关于直线DE的对称,
∴DF=DG,
正方形ABCD中,∵AD=CD,∠ADC=∠A=∠BCD=90°,
∴∠GCD=90°,又在Rt△AFD与Rt△CDG中,
|
∴Rt△AFD≌Rt△CDG,
∴∠ADF=∠CDG,
∴∠FDG=∠ADC=90°,
∴△FDG是等腰直角三角形,
∵DH⊥CF,
∴DH=FH=
| 1 |
| 2 |
∵HP⊥AB,HQ⊥AD,∠A=90°,
∴四边形APHQ是矩形,
∴∠PHQ=90°,
∵∠DHF=90°,
∴∠PHF=∠DHQ,又在△PFF与△DQH中有
|
∴△HPF≌△DHQ,
∴HP=HQ,所以矩形APHQ是正方形;
设正方形APHQ边长为a,则在Rt△MQH中,有(a-3)2+a2=17,解得a=4;
∴FP=QD=AD-AQ=6-4=2,
又易证△FPH∽△EHG,则有
| EG |
| FH |
| GH |
| PH |
| FH2 |
| PH |
又FH2=22+42=20,PH=4,
∴EG=5
故答案为:5.
看了 如图,边长为6的正方形ABC...的网友还看了以下:
根据下面条件,能组成平行四边形的是A相邻两边分别是4cm和5cm,且一条对角线长10cmB一边长为 2020-06-02 …
一个正方形被3四条平行于一组对边和4条平行于另一组对边的线段,分成大小不同的20个小长方形.这些小 2020-06-03 …
一个正方形被4条平行于一组对边和5条平行于另一组对边的线段分割成了30个大小不同的长方形,这些长方 2020-06-03 …
已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半以四边形ABCD 2020-06-06 …
1一条弧线,已知弧高45公分,弦长180公分,求出圆心点焦距弧长2一个直角三角形,邻边90公分,三 2020-07-26 …
正六边形,对边距离为60mm,求边长,请各位大大告诉我算出来的方法流年你的算法是错误的,我说的是对 2020-07-30 …
给出下列命题:(1)一组对边和一组对角分别相等的四边形是平行四边形;(2)两组对角的内角平分线分别 2020-07-30 …
一道关于正五边形的题五边形边长为3,求一个顶点到对边的线段的长 2020-08-01 …
我有道数学题不会做,帮我解决好吗?我在线,知道的马上回答我马红家有一块边长是15米的正方形菜田地.今 2020-11-19 …
三角形的高就是顶点到对边垂线段的长度,这句话对吗?教科书上的定义是:从三角形的一个顶点向它的对边所在 2021-01-08 …