如图，抛物线y=ax2+2x+c经过点A（0，3），B（-1，0），请解答下列问题：（1）求抛物线的解析式；（2）抛物线的顶点为D，对称轴与x轴交于点E，点A关于DE的对称点为M，连接BM，求BM的长．注：

Question

如图，抛物线y=ax²+2x+c经过点A（0，3），B（-1，0），请解答下列问题：

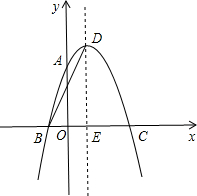
（1）求抛物线的解析式；
（2）抛物线的顶点为D，对称轴与x轴交于点E，点A关于DE的对称点为M，连接BM，求BM的长．
注：抛物线y=ax²+bx+c（a≠0）的顶点坐标是（-(b)/(2a)，(4ac-b2)/(4a)）

Answer 1

（1）∵抛物线y=ax²+2x+c经过点A（0，3），B（-1，0），
∴将A（0，3），B（-1，0）代入得：

3=c

0=a-2+c

，
解得：

a=-1

c=3

．
则抛物线解析式为y=-x²+2x+3；
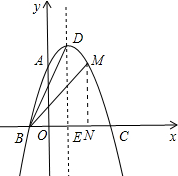（2）由顶点坐标（-(b)/(2a)，(4ac-b2)/(2a)）得：D（1，4），
∵抛物线的对称轴与x轴交于点E，
∴OE=1，
∴对称轴为x=1，
∵点A关于DE的对称点为M，
∴M（2，3），
如图所示：过点M作MN⊥x轴于点N，
则N（2，0），
∴BN=3，MN=3，
在Rt△BMN中，根据勾股定理得：BM=√(MN2+BM2)=√(32+32)=3√(2)．