早教吧作业答案频道 -->数学-->
如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.(1)求此抛物线的解析
题目详情
如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
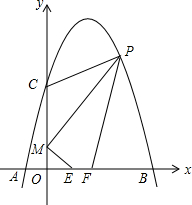
(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标.

(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标.
▼优质解答
答案和解析
(1)∵对称轴为直线x=2,
∴设抛物线解析式为y=a(x-2)2+k.
将A(-1,0),C(0,5)代入得:
,
解得
,
∴y=-(x-2)2+9=-x2+4x+5.
(2)当a=1时,E(1,0),F(2,0),OE=1,OF=2.
设P(x,-x2+4x+5),
如答图2,过点P作PN⊥y轴于点N,则PN=x,ON=-x2+4x+5,
∴MN=ON-OM=-x2+4x+4.
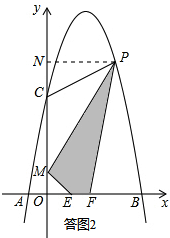
S四边形MEFP=S梯形OFPN-S△PMN-S△OME
=
(PN+OF)•ON-
PN•MN-
OM•OE
=
(x+2)(-x2+4x+5)-
x•(-x2+4x+4)-
×1×1
=-x2+
x+
=-(x-
)2+
,
∴当x=
时,四边形MEFP的面积有最大值为
,
把x=
时,y=-(
-2)2+9=
.
此时点P坐标为(
,
).
∴设抛物线解析式为y=a(x-2)2+k.
将A(-1,0),C(0,5)代入得:
|
解得
|
∴y=-(x-2)2+9=-x2+4x+5.
(2)当a=1时,E(1,0),F(2,0),OE=1,OF=2.
设P(x,-x2+4x+5),
如答图2,过点P作PN⊥y轴于点N,则PN=x,ON=-x2+4x+5,
∴MN=ON-OM=-x2+4x+4.

S四边形MEFP=S梯形OFPN-S△PMN-S△OME
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-x2+
| 9 |
| 2 |
| 9 |
| 2 |
=-(x-
| 9 |
| 4 |
| 153 |
| 16 |
∴当x=
| 9 |
| 4 |
| 153 |
| 16 |
把x=
| 9 |
| 4 |
| 9 |
| 4 |
| 143 |
| 16 |
此时点P坐标为(
| 9 |
| 4 |
| 143 |
| 16 |
看了 如图,对称轴为直线x=2的抛...的网友还看了以下:
英语翻译英文翻译成中文:1.经历5天苦寻,这位女士终于在废墟中找到了母亲,而两人已是阴阳相隔.这位 2020-05-17 …
在鸡的杂交实验中,已知鸡的毛腿(F)对光腿(f)是显性,豌豆冠(E)对单冠(e)是显性。A、B两只 2020-06-08 …
ABCDE五个好朋友节日互相打电话问候,每两人互相通话一次.到现在为止,A已通话4次,B已通话3次 2020-06-16 …
一词多义然志犹未已,今操已拥百万之众的两个已是什么意思 2020-06-18 …
一题数学题``已知细菌繁殖是一个细菌分裂成两个,一个细菌分裂a次后,数量变为2^a个.(1)E.C 2020-06-26 …
已知四边形ABCD中,∠ABC=120°∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD, 2020-07-07 …
⒈点C在线段AB上,线段AC=6cmBC=4cm,点M,N分别是AC,BC中点,求线段MN的长度. 2020-07-30 …
已知椭圆C:x2/a2+y2/b2=1(a>b>0)的离心率e=根6/3过点A(0,-b)和B(a 2020-07-30 …
A、B、C、D、E、F六个组球队一起进行比赛,每两队都要比赛一场,到现在为止,A已赛5场,B已赛4场 2020-10-31 …
已知EUF包含于{4,5,6,7,8,9},求所有(E,F)的个数(E,F)是指一个集对.所谓集对, 2020-11-20 …