早教吧作业答案频道 -->数学-->
课本上的探索与研究中有这样一个问题:已知△ABC的面积为S,外接圆的半径为R,∠A,∠B,∠C的对边分别为a,b,c,用解析几何的方法证明:R=abc4S.小东根据学习解析
题目详情
课本上的探索与研究中有这样一个问题:
已知△ABC的面积为S,外接圆的半径为R,∠A,∠B,∠C的对边分别为a,b,c,用解析几何的方法证明:R=
.
小东根据学习解析几何的经验,按以下步骤进行了探究:
(1)在△ABC所在的平面内,建立直角坐标系,使得△ABC三个顶点的坐标的表示形式较为简单,并设出表示它们坐标的字母;
(2)用表示△ABC三个顶点坐标的字母来表示△ABC的外接圆半径、△ABC的三边和面积;
(3)根据上面得到的表达式,消去表示△ABC的三个顶点的坐标的字母,得出关系式.
在探究过程中,小东遇到了以下问题,请你帮助完成:
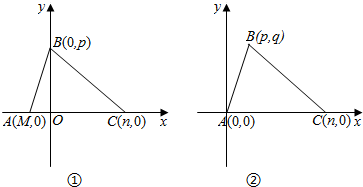
(Ⅰ)为了△ABC的三边和面积表达式及外接圆方程尽量简单,小东考虑了如下两种建系方式;你选择第___种建系方式.
(Ⅱ)根据你选择的建系方式,完成以下部分探究过程:
(1)设△ABC的外接圆的一般式方程为x2+y2+Dx+___=0;
(2)在求解圆的方程的系数时,小东观察图形发现,由圆的几何性质,可以求出圆心的横坐标为___,进而可以求出D=___;
(3)外接圆的方程为___.
已知△ABC的面积为S,外接圆的半径为R,∠A,∠B,∠C的对边分别为a,b,c,用解析几何的方法证明:R=
| abc |
| 4S |
小东根据学习解析几何的经验,按以下步骤进行了探究:
(1)在△ABC所在的平面内,建立直角坐标系,使得△ABC三个顶点的坐标的表示形式较为简单,并设出表示它们坐标的字母;
(2)用表示△ABC三个顶点坐标的字母来表示△ABC的外接圆半径、△ABC的三边和面积;
(3)根据上面得到的表达式,消去表示△ABC的三个顶点的坐标的字母,得出关系式.
在探究过程中,小东遇到了以下问题,请你帮助完成:
(Ⅰ)为了△ABC的三边和面积表达式及外接圆方程尽量简单,小东考虑了如下两种建系方式;你选择第___种建系方式.
(Ⅱ)根据你选择的建系方式,完成以下部分探究过程:
(1)设△ABC的外接圆的一般式方程为x2+y2+Dx+___=0;
(2)在求解圆的方程的系数时,小东观察图形发现,由圆的几何性质,可以求出圆心的横坐标为___,进而可以求出D=___;
(3)外接圆的方程为___.

▼优质解答
答案和解析
设△ABC的外接圆的一般式方程为x2+y2+Dx+Ey+F=0,则D=-m-n,
∴方程为x2+y2+(-m-n)x+Ey+F=0,
代入(0,p),(n,0),可得
,
∴F=mn,E=-p-
,
∴外接圆的方程为x2+y2+(-m-n)x+(-p-
)y+mn=0.
故答案为:①;Ey+F;
;-m-n;x2+y2+(-m-n)x+(-p-
)y+mn=0.
∴方程为x2+y2+(-m-n)x+Ey+F=0,
代入(0,p),(n,0),可得
|
∴F=mn,E=-p-
| mn |
| p |
∴外接圆的方程为x2+y2+(-m-n)x+(-p-
| mn |
| p |
故答案为:①;Ey+F;
| m+n |
| 2 |
| mn |
| p |
看了 课本上的探索与研究中有这样一...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
在平行四边形ABCD中,∠A=π/3,边AB,AD的长分别为4,2,若M,N分别是边BC,CD上的 2020-05-13 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
等边三角形中的高与它的边比较,().A高比边短B高比边长C一样等边三角形中的高与它的边比较,(). 2020-06-05 …
在△ABC中,∠=90°,锐角A的对边与邻边的比叫做∠A正切,记作tanA,即tanA=邻边分子∠ 2020-06-18 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
把(a-b)-2b+2a分解因式甲同学的解=A²-2AB+B²-2B+2A=A²+2A-2AB+B 2020-07-15 …
能够铺满地面的正多边形的组合是?A.正八边形和正方形B.正七边形和正十边形C.正方形和正六边形D. 2020-07-30 …
等腰三角形顶角的外角平分线与底边的关系是什么?到三角形三边的距离相等的点是A三边的垂直平分线的交点 2020-08-03 …