早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,∠BAC=45°,以AB为直径的⊙O交BC于点D,交AC于点E.(1)求∠EBC的度数;(2)求证:BD=CD.
题目详情
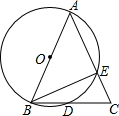 如图,在△ABC中,AB=AC,∠BAC=45°,以AB为直径的⊙O交BC于点D,交AC于点E.
如图,在△ABC中,AB=AC,∠BAC=45°,以AB为直径的⊙O交BC于点D,交AC于点E.(1)求∠EBC的度数;
(2)求证:BD=CD.
▼优质解答
答案和解析
考点:
圆周角定理 全等三角形的判定与性质 等腰三角形的性质
专题:
计算题
分析:
(1)根据等腰三角形的性质得∠ABC=∠C,再利用三角形内角和计算出∠C=12(180°-∠BAC)=67.5°,接着根据圆周角定理得∠AEB=90°,然后利用三角形外角性质求∠EBC的度数;(2)连结AD,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,然后根据等腰三角形的性质即可得到BD=CD.
(1)∵AB=AC,∴∠ABC=∠C,∴∠C=12(180°-∠BAC)=12(180°-45°)=67.5°,∵AB为直径,∴∠AEB=90°,∵∠AEB=∠EBC+∠C,∴∠EBC=90°-67.5°=22.5°;(2)证明:连结AD,如图,∵AB为直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=CD.
点评:
本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的性质.
考点:
圆周角定理 全等三角形的判定与性质 等腰三角形的性质
专题:
计算题
分析:
(1)根据等腰三角形的性质得∠ABC=∠C,再利用三角形内角和计算出∠C=12(180°-∠BAC)=67.5°,接着根据圆周角定理得∠AEB=90°,然后利用三角形外角性质求∠EBC的度数;(2)连结AD,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,然后根据等腰三角形的性质即可得到BD=CD.
(1)∵AB=AC,∴∠ABC=∠C,∴∠C=12(180°-∠BAC)=12(180°-45°)=67.5°,∵AB为直径,∴∠AEB=90°,∵∠AEB=∠EBC+∠C,∴∠EBC=90°-67.5°=22.5°;(2)证明:连结AD,如图,∵AB为直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=CD.
点评:
本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的性质.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
仿写句子有的石钟乳如天马行空如什么如什么有的如什么? 2020-05-13 …
一个单人旁加一个如果的如字念什么?一个单人旁右边加一个如果的如字念什么字?我用五笔和拼音都打不出来 2020-05-14 …
请问“#”“*”“-”英语中怎么读?1.比如拨打电话时,对方说:请按“#”“*”键……该如何用英语 2020-05-17 …
如图所示,倾角 =30度粗糙斜面上放一个物体,物体重为G,静止在斜面上 (1)如果用一个与斜面底边 2020-05-17 …
带有比喻意义的,()()如()带有比喻意义的,()()如(),如:洁白如雪 2020-05-23 …
我对数字,没什么概念.我想问一下百分之几这个应该怎么算?比如:2.6%就是:以0.026相乘,这个 2020-06-05 …
“杀人如不能举,刑人如恐不胜”中的“如”如何解释? 2020-06-12 …
兢兢业业,如霆如雷.中的“如霆如雷”什么意思? 2020-06-16 …
依据《现代汉语词典》给出的义项,下面词语的“如”字的正确释是:1适合,依据2如同3及,比得上4表示 2020-06-21 …
进位标志位CF在做减法时是如何置数的做减法时,对减数求补,然后做加法,这时是如何置位的?如2-1, 2020-07-07 …