早教吧作业答案频道 -->数学-->
如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.(1)求证:△CAE∽△CBF;(2)若BE=1,AE=2,求CE的长.
题目详情
如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.
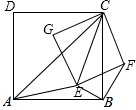
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.

(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD和EFCG均为正方形,
∴
=
=
,
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2) ∵△CAE∽△CBF,
∴∠CAE=∠△CBF,
=
,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵
=
=
,AE=2
∴
=
,
∴BF=
,
∴EF2=BE2+BF2=3,
∴EF=
,
∵CE2=2EF2=6,
∴CE=
.
∴
| AC |
| BC |
| CE |
| CF |
| 2 |
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2) ∵△CAE∽△CBF,
∴∠CAE=∠△CBF,
| AE |
| BF |
| AC |
| BC |
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵
| AE |
| BF |
| AC |
| BC |
| 2 |
∴
| 2 |
| BF |
| 2 |
∴BF=
| 2 |
∴EF2=BE2+BF2=3,
∴EF=
| 3 |
∵CE2=2EF2=6,
∴CE=
| 6 |
看了 如图,已知AC,EC分别为正...的网友还看了以下:
补全下列推理过程:如图,已知AB∥CE,∠A=∠E,求证:∠CGD=∠FHB如图,已知AB∥CE( 2020-04-25 …
如图是某植物叶肉细胞中光合作用与呼吸作用之间的关系图,其中A~E表示相关过程,a~e表示相关物质, 2020-05-14 …
MATLAB 如何赋值 画实部虚部图像 画图clearclcsyms a j k n u e A 2020-05-16 …
已知,如图,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=x分之3的图像经过点A、E 2020-05-17 …
在E-R图和数据流图中都使用了方框,下列说法中有错误的是( )。A.在E-R图中表示实体B.在E-R 2020-05-23 …
在E-R图和数据流图中都使用了方框,下列说法中有错误的是______。A.在E-R图中表示实体B.在 2020-05-24 …
设G=为无环的无向图,|V|=6,|E|=16,则G是()A.完全图B.零图C.D.多重图设A和B 2020-06-12 …
若对任意e>0,在数列{Xn}中有无数个点落在a的e领域内,能否说Xn→a?若不成立,请举出反例. 2020-06-12 …
(1)如图①∵∠B+∠D+∠1=180°又∵∠1=∠A+∠2∠2=∠C+∠E∴∠A+∠C+∠E+∠ 2020-06-13 …
(2011•桐乡市二模)(1)尝试:如图,已知A、E、B三点在同一直线上,且∠A=∠B=∠DEC= 2020-06-16 …