早教吧作业答案频道 -->数学-->
在长方体ABCD-A1B1C1D1中,底面边长AB=3m,BC=4m,高BB1=5m,求:(1)写出B1D、BC1在平面ABCD内的射影;(2)对角线DB1与平面ABCD所成角的大小;(3)BC1与平面ABCD所成角的正切.
题目详情
在长方体ABCD-A1B1C1D1中,底面边长AB=3m,BC=4m,高BB1=5m,求:
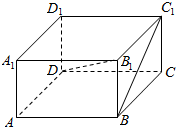
(1)写出B1D、BC1在平面ABCD内的射影;
(2)对角线DB1与平面ABCD所成角的大小;
(3)BC1与平面ABCD所成角的正切.

(1)写出B1D、BC1在平面ABCD内的射影;
(2)对角线DB1与平面ABCD所成角的大小;
(3)BC1与平面ABCD所成角的正切.
▼优质解答
答案和解析
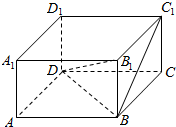 (1)∵B1B⊥平面ABCD,垂足为B,
(1)∵B1B⊥平面ABCD,垂足为B,
∴B1D在平面ABCD内的射影为BD;
∵C1C⊥平面ABCD,垂足为C,
∴BC1在平面ABCD内的射影为BC.
(2)∵B1B⊥平面ABCD,垂足为B,B1D在平面ABCD内的射影为BD,
∴∠B1DB是对角线DB1与平面ABCD所成角,
∵在长方体ABCD-A1B1C1D1中,底面边长AB=3m,BC=4m,高BB1=5m,
∴BD=
=5(m),
∴tan∠B1DB=
=
=1,∴∠B1DB=45°,
∴对角线DB1与平面ABCD所成角的大小为45°.
(3)∵C1C⊥平面ABCD,垂足为C,BC1在平面ABCD内的射影为BC,
∴∠C1BC是BC1与平面ABCD所成角,
tan∠C1BC=
=
,
∴BC1与平面ABCD所成角的正切为
.
 (1)∵B1B⊥平面ABCD,垂足为B,
(1)∵B1B⊥平面ABCD,垂足为B,∴B1D在平面ABCD内的射影为BD;
∵C1C⊥平面ABCD,垂足为C,
∴BC1在平面ABCD内的射影为BC.
(2)∵B1B⊥平面ABCD,垂足为B,B1D在平面ABCD内的射影为BD,
∴∠B1DB是对角线DB1与平面ABCD所成角,
∵在长方体ABCD-A1B1C1D1中,底面边长AB=3m,BC=4m,高BB1=5m,
∴BD=
| 9+16 |
∴tan∠B1DB=
| BB1 |
| BD |
| 5 |
| 5 |
∴对角线DB1与平面ABCD所成角的大小为45°.
(3)∵C1C⊥平面ABCD,垂足为C,BC1在平面ABCD内的射影为BC,
∴∠C1BC是BC1与平面ABCD所成角,
tan∠C1BC=
| CC1 |
| BC |
| 5 |
| 4 |
∴BC1与平面ABCD所成角的正切为
| 5 |
| 4 |
看了 在长方体ABCD-A1B1C...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
在一定温度下,化学平衡常数K=(C)c(D)d / (A)a(B)b.给定AB的浓度 达到平衡 就 2020-04-06 …
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
1命题若a=x/4则tana=1的逆否命题是2设集合A=(a,b)b=(b,c,d)则AUB=3若 2020-08-02 …
100%收购公司其中一名法人股东涉及到的问题事实:A.B.C.D为四个法人。A.B公司为C公司的股东 2020-11-06 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …