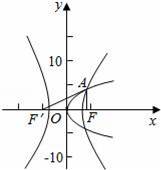
已知抛物线y2=4px（p＞0）与双曲线有相同的焦点F，点A是两曲线的交点，且AF⊥x轴，则双曲线的离心率为（）A．B．C．D．

Question

已知抛物线y²=4px（p＞0）与双曲线有相同的焦点F，点A是两曲线的交点，且AF⊥x轴，则双曲线的离心率为（　　）

A．    B．    C．    D．

Answer 1

b【考点】双曲线的简单性质．

【专题】计算题；圆锥曲线的定义、性质与方程．

【分析】设双曲线的左焦点为F'，连接AF'，由抛物线方程求得A（p，2p），结合双曲线的焦距，得到△AFF'是以AF'为斜边的等腰直角三角形．再根据双曲线定义，得实轴2a=2p（），而焦距2c=2p，由离心率公式可算出该双曲线的离心率．

【解答】设双曲线的左焦点为F'，连接AF'

∵F是抛物线y²=4px的焦点，且AF⊥x轴，

∴设A（p，y₀），得y₀²=4p×p，得y₀=2p，A（p，2p），

因此，Rt△AFF'中，|AF|=|FF'|=2p，得|AF'|=2p

∴双曲线的焦距2c=|FF'|=2p，实轴2a=|AF'|﹣|AF|=2p（）

由此可得离心率为：e====

故选：B

【点评】本题给出双曲线与抛物线有共同的焦点，求双曲线的离心率，着重考查了双曲线、抛物线的定义与简单几何性质等知识，属于中档题．