若双曲线x2a2-y2b2=1（a>0，b>0）的一条渐近线与x24+y23=1的交点在x轴上的射影恰为该椭圆的焦点，则双曲线的

Question

若双曲线 (x2)/(a2)- (y2)/(b2)=1（a>0，b>0）的一条渐近线与 (x2)/(4)+ (y2)/(3)=1的交点在x轴上的射影恰为该椭圆的焦点，则双曲线的离心率为___．

Answer 1

椭圆(x2)/(4)+(y2)/(3)=1的焦点坐标为（±1，0），
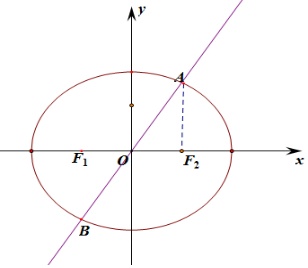
设渐近线y=(b)/(a)x与椭圆(x2)/(4)+(y2)/(3)=1交于A（x₁，y₁），B（-x₁，-y₁）两点，
则x₁=1，解得：y₁=(3)/(2)，则A（1，(3)/(2)），
代入渐近线方程整理得：(b)/(a)=(3)/(2)，
双曲线的离心率e=(c)/(a)=√(1+(b2)/(a2))=(√(13))/(2)，
故答案为：(√(13))/(2)．