设函数f（x）=ex（x-aex）（其中e为自然对数的底数）恰有两个极值点x1，x2（x1<x2），则下列说法不正确的是（）A.0<a<12B.-1<x1<0C.-12<f（x1）<0D.f（x1）+f（x2）>0

Question

设函数f（x）=e^x（x-ae^x）（其中e为自然对数的底数）恰有两个极值点x₁，x₂（x₁<x₂），则下列说法不正确的是（　　）

A. 0<a<

(1)/(2)

B. -1<x₁<0

C. -

(1)/(2)<f（x₁）<0

D. f（x₁）+f（x₂）>0

Answer 1

∵函数f（x）=e^x（x-ae^x），
∴f′（x）=（x+1-2a•e^x）e^x，
由于函数f（x）的两个极值点为x₁，x₂，
即x₁，x₂是方程f′（x）=0的两不等实根，
即方程x+1-2ae^x=0，且a≠0，
∴(x+1)/(2a)=e^x；
设y₁=(x+1)/(2a)（a≠0），y₂=e^x，
在同一坐标系内画出这两个函数的图象，如图所示；

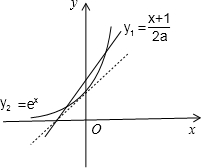
要使这两个函数有2个不同的交点，
应满足

(1)/(2a)>0

(1)/(2a)>1

，
解得0<a<(1)/(2)，
所以a的取值范围是（0，(1)/(2)），
结合图象，D错误，
故选：D．