早教吧作业答案频道 -->数学-->
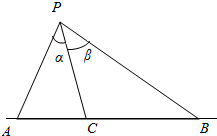
如图,一条直线上有三点A,B,C,点C在点A与点B之间,点P是此直线外一点,设∠APC=α,∠BPC=β.求证:sin(α+β)PC=sinαPB+sinβPA.
题目详情
如图,一条直线上有三点A,B,C,点C在点A与点B之间,点P是此直线外一点,设∠APC=α,∠BPC=β.求证:
=
+
.
| sin(α+β) |
| PC |
| sinα |
| PB |
| sinβ |
| PA |

▼优质解答
答案和解析
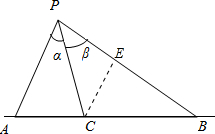 证明:过点C作CE∥PA,交PB于点E,则∠PCE=α,∠PEC=π-(α+β),
证明:过点C作CE∥PA,交PB于点E,则∠PCE=α,∠PEC=π-(α+β),
则在△PCE中,由正弦定理得:
=
=
,
即
=
=
,
∴
=
=
,
利用比例性质,有:
=
,
∵CE∥PA,
∴CE:PA=BE:PB,
∴PA•PE+PB•CE=PA•PE+PA•BE=PA•(PE+BE)=PA•PB,
则
=
+
.
 证明:过点C作CE∥PA,交PB于点E,则∠PCE=α,∠PEC=π-(α+β),
证明:过点C作CE∥PA,交PB于点E,则∠PCE=α,∠PEC=π-(α+β),则在△PCE中,由正弦定理得:
| sin∠PEC |
| PC |
| sin∠PCE |
| PE |
| sin∠BPC |
| CE |
即
| sin[π-(α+β)] |
| PC |
| sinα |
| PE |
| sinβ |
| CE |
∴
| sin(α+β) |
| PC |
| PA•sinα |
| PA•PE |
| PB•sinβ |
| PB•CE |
利用比例性质,有:
| sin(α+β) |
| PC |
| PAsinα+PBsinβ |
| PA•PE+PB•CE |
∵CE∥PA,
∴CE:PA=BE:PB,
∴PA•PE+PB•CE=PA•PE+PA•BE=PA•(PE+BE)=PA•PB,
则
| sin(α+β) |
| PC |
| sinα |
| PB |
| sinβ |
| PA |
看了 如图,一条直线上有三点A,B...的网友还看了以下:
在循环双链表的p所指节点之后插入s所直接点操作A,p->next=s;s->prior=p;p->n 2020-03-31 …
注意你的“体语”(阅读题)注意你的“体语”①日常生活中,我们的一举一动,一pín一笑,往往是其心迹 2020-04-26 …
下列对应法则f中,构成从集合P到S的映射的是()A.P=R,S=(-∞,0),x∈P,y∈S,f: 2020-06-23 …
下列对应法则f中,构成从集合P到S的映射的是AP=R,S=(-∞,0),x∈P,y∈S,f:x→y 2020-07-30 …
已知全集S和集合M,N,P.M=N在S中的补集N=P在S中的补集,则M与P的关系是?A、M=P在S 2020-07-30 …
任何一个正整数n都可以进行这样的分解:n=s×t(s、t是正整数,且s≤t),如果p×q在n的所有 2020-07-31 …
任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有 2020-07-31 …
任何一个正整数n都可以进行这样的分解:n=s×t(s、t是正整数,且s≤t),如果p×q在n的所有这 2020-12-01 …
1.以知集合A=『2n/n∈Z』,B=『4n+2,4n-2/n∈Z』,则集合A、B之间的关系是什么? 2020-12-07 …
英语:下1.将下联打乱的字母组成单词,并写出汉语意思1.a,e,h,g,c,n[]2.e,i,s,t 2020-12-10 …