早教吧作业答案频道 -->数学-->
平移、旋转、翻折是几何图形的最基本的三种图形变换,利用图形变换可将分散的条件相对集中,以达到解决问题的目的.(1)探究发现如图(1),P是等边△ABC内一点,PA=3,PB=4,PC=5.求
题目详情
平移、旋转、翻折是几何图形的最基本的三种图形变换,利用图形变换可将分散的条件相对集中,以达到解决问题的目的.
(1)探究发现
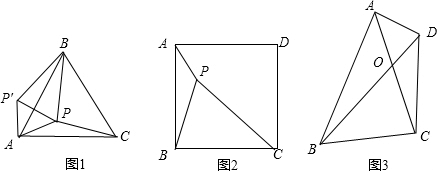
如图(1),P是等边△ABC内一点,PA=3,PB=4,PC=5.求∠APB的度数.
将△APC绕点A旋转到△APB′的位置,连接PP′,则△APP′是___三角形.
∵PP′=PA=3,PB=4,PB′=PC=5,
∴P'P2+PB2=P'B2∴△BPP′为___三角形.∴∠APB的度数为___.
(2)类比延伸
在正方形ABCD内部有一点P,连接PA、PB、PC,若PA=2,PB=4,∠APB=135°,求PC的长;
(3)拓展迁移
如图(3),在四边形ABCD中,线段AD与BC不平行,AC=BD=a,AC与BD交于点O,且∠AOD=60°,比较AD+BC与a的大小关系,并说明理由.

(1)探究发现
如图(1),P是等边△ABC内一点,PA=3,PB=4,PC=5.求∠APB的度数.
将△APC绕点A旋转到△APB′的位置,连接PP′,则△APP′是___三角形.
∵PP′=PA=3,PB=4,PB′=PC=5,
∴P'P2+PB2=P'B2∴△BPP′为___三角形.∴∠APB的度数为___.
(2)类比延伸
在正方形ABCD内部有一点P,连接PA、PB、PC,若PA=2,PB=4,∠APB=135°,求PC的长;
(3)拓展迁移
如图(3),在四边形ABCD中,线段AD与BC不平行,AC=BD=a,AC与BD交于点O,且∠AOD=60°,比较AD+BC与a的大小关系,并说明理由.
▼优质解答
答案和解析
将△APC绕点A旋转到△APB′的位置,连接PP′,则△APP′是等边三角形.
∵PP′=PA=3,PB=4,PB′=PC=5,
∴P'P2+PB2=P'B2,
∴△BPP′为直角三角形,
∴∠APB的度数为90°+60°=150°
故答案为:等边;直角;150°
(2)如图1,把△ABP绕点B顺时针旋转90°得到△BCP′,
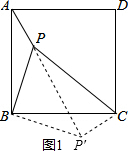
则P′B=PB=4,P′C=PA=2,
∵旋转角是90°,
∴∠PBP′=90°,
∴△BPP′是等腰直角三角形,
∴PP′=
PB=4
,∠PP′B=45°,
∵∠APB=135°,
∴∠CP′B=∠APB=135°,
∴∠PP′C=135°-45°=90°,
在Rt△PP′C中,由勾股定理得,PC=
=
=6;
(3)AD+BC>a,理由如下:
如图2所示,以AC为边向左做等边三角形PAC,连接PB,
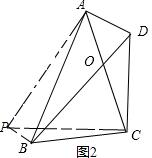
则PA=PC=AC=BD=a,∠PAC=60°,
∵∠AOD=60°,
∴PA∥BD,
∴四边形APBD是平行四边形,
∴AD=PB,
在△PBC中,可得:PB+BC>PC,即AD+BC>a.
∵PP′=PA=3,PB=4,PB′=PC=5,
∴P'P2+PB2=P'B2,
∴△BPP′为直角三角形,
∴∠APB的度数为90°+60°=150°
故答案为:等边;直角;150°
(2)如图1,把△ABP绕点B顺时针旋转90°得到△BCP′,

则P′B=PB=4,P′C=PA=2,
∵旋转角是90°,
∴∠PBP′=90°,
∴△BPP′是等腰直角三角形,
∴PP′=
| 2 |
| 2 |
∵∠APB=135°,
∴∠CP′B=∠APB=135°,
∴∠PP′C=135°-45°=90°,
在Rt△PP′C中,由勾股定理得,PC=
| PP′2+P′C2 |
(4
|
(3)AD+BC>a,理由如下:
如图2所示,以AC为边向左做等边三角形PAC,连接PB,

则PA=PC=AC=BD=a,∠PAC=60°,
∵∠AOD=60°,
∴PA∥BD,
∴四边形APBD是平行四边形,
∴AD=PB,
在△PBC中,可得:PB+BC>PC,即AD+BC>a.
看了 平移、旋转、翻折是几何图形的...的网友还看了以下:
下列情况中的物体,哪些可以看成质点A研究绕地球飞行时的航天飞机B研究从桥上通过的一列队伍C研究在水 2020-04-25 …
下列运用科学方法的实例中,正确的是()A.把固体分成晶体和非晶体,运用了类比法B.研究平面镜成像时 2020-05-02 …
物理研究中常常用到“转换法”“控制变量法”“模型法”“类比法”等方法,下面几个实验中,采用了控制变 2020-05-02 …
一科学兴趣小组在探究二力平衡条件时,将小车放在光滑的水平桌面上,两边分别用细线通过定滑轮与重物A、 2020-05-17 …
地租是土地所有者凭借土地所有权向土地使用者让渡土地使用权时索取的( )A.平均利润 B.边际收益 2020-05-19 …
下列有关群落的叙述,错误的是()A.研究种群是研究群落的基础B.不同群落的物种数目是不同的C.群落 2020-05-22 …
一般所说的流速是指同一断面上的( )A.平均流速B.最小流速C.水面流速D.最大流速 2020-05-27 …
土壤的稳定渗吸速度又叫土壤的()A.平均入渗速度B.渗吸水量C.渗透系数D.渗吸速度 2020-05-28 …
北极形成阴霾天气主要原因是北极的A.平均气温比南极高B.海冰比南极多C.相对湿度比南极大理由呢 2020-06-05 …
物质资料生产是政治经济学研究的( )A.落脚点 B.着重点 C.出发点 D.中介点 2020-06-06 …