早教吧作业答案频道 -->数学-->
如图,有两条互相平行的直线l1,l2,点A,B在直线l1上,点D,C在直线l2上,连接AD,BC.已知∠ADC=90°,AB=3,DC=6,BC=5.点E是线段DC上任意一点,点F在线段AB的延长线上,且AE=AF,连接EF,与线
题目详情
如图,有两条互相平行的直线l1,l2,点A,B在直线l1上,点D,C在直线l2上,连接AD,BC.已知∠ADC=90°,AB=3,DC=6,BC=5.点E是线段DC上任意一点,点F在线段AB的延长线上,且AE=AF,连接EF,与线段BC相交于点G.
(1)求线段AD的长;
(2)求线段BF最大值与最小值;
(3)连接BE,FC,当BE∥CF时,求BF的长.
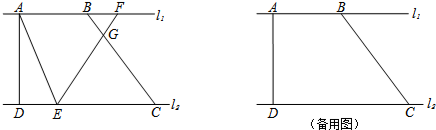
(1)求线段AD的长;
(2)求线段BF最大值与最小值;
(3)连接BE,FC,当BE∥CF时,求BF的长.
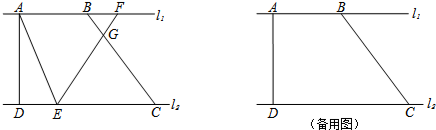
▼优质解答
答案和解析
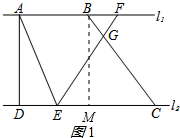 (1)作BM⊥CD于M,如图1所示:
(1)作BM⊥CD于M,如图1所示:
∵∠ADC=90°,
∴BM∥AD,
∵l1∥l2,
∴四边形ADMB是矩形,
∴AD=BM,DM=AB=3,
∴CM=DC-DM=3,
∴AD=BM=
=
=4;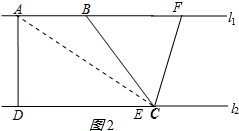
(2)当点E与C重合时,BF有最大值,连接AC,如图2所示:
则AE=AC=
=
=2
,
∴AF=AE=2
,BF的最大值=2
-3;
当点E与D重合时,BF有最小值,
∵AF=AE=AD=4,
∴BF的最小值=4-3=1;
(3)如图3所示:当BE∥CF时,四边形BECF是平行四边形,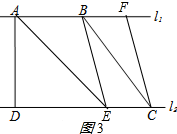
∴BF=CE,
设BF=CE=x,则AE=AF=AB+BF=3+x,DE=DC-CE=6-x,
在Rt△ADE中,由勾股定理得:AD2+DE2=AE2,
即42+(6-x)2=(x+4)2,
解得:x=1.8,
即BF的长为1.8.
 (1)作BM⊥CD于M,如图1所示:
(1)作BM⊥CD于M,如图1所示:∵∠ADC=90°,
∴BM∥AD,
∵l1∥l2,
∴四边形ADMB是矩形,
∴AD=BM,DM=AB=3,
∴CM=DC-DM=3,
∴AD=BM=
| BC2-CM2 |
| 52-32 |

(2)当点E与C重合时,BF有最大值,连接AC,如图2所示:
则AE=AC=
| AD2+DC2 |
| 42+62 |
| 13 |
∴AF=AE=2
| 13 |
| 13 |
当点E与D重合时,BF有最小值,
∵AF=AE=AD=4,
∴BF的最小值=4-3=1;
(3)如图3所示:当BE∥CF时,四边形BECF是平行四边形,

∴BF=CE,
设BF=CE=x,则AE=AF=AB+BF=3+x,DE=DC-CE=6-x,
在Rt△ADE中,由勾股定理得:AD2+DE2=AE2,
即42+(6-x)2=(x+4)2,
解得:x=1.8,
即BF的长为1.8.
看了 如图,有两条互相平行的直线l...的网友还看了以下:
提示:D-C=0A-B,A-D,D-C,D-E,E-F=1A-D,C-F=2A-B,D-E,E-F 2020-04-06 …
把下面的式子写成(A+B)(A-B)的形式(1)(a+b+c+d)(-a-b+c+d)(2)(把下 2020-04-27 …
已知有序数组(a,b,c,d),现按下列方式重新写成数组(a1,b1,c1,d1)使a1=a+b, 2020-05-13 …
已知a/b=c/d=e/f=2,当b+d≠0时,a+c/b+d=;当b+d+f≠0时,a+c+e/ 2020-05-14 …
#includemain(){inta=0x7fffffff,b=025;floatf1=123. 2020-05-19 …
大脑沟回的作用,意义A.增加了大脑皮层的总面积 B.增加了大脑皮层神经细胞的数量C.A或B D.A 2020-06-27 …
外出野营一定要注意安全,山中不适合露营的地点是,原因是()A.D处D处为山谷,下暴雨易形成山洪B. 2020-07-05 …
求表达式!任意输入一个三位数abc,则由abc如何求出bca?小弟写的:includevoidma 2020-07-23 …
若有以下程序#include“stdio.h”main(){inta=1,b=2,c=3,d=4; 2020-07-23 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …