早教吧作业答案频道 -->数学-->
阅读理解如图(1),在正多边形A1A2A3…An的边A2A3上任取一不与点A2重合的点B2,并以线段A1B2为边在线段A1A2的上方作以正多边形A1B2B3…Bn,把正多边形A1B2B3…Bn叫正多边形A1A2…An的准位似图形
题目详情
阅读理解
如图(1),在正多边形A1A2A3…An的边A2A3上任取一不与点A2重合的点B2,并以线段A1B2为边在线段A1A2的上方作以正多边形A1B2B3…Bn,把正多边形A1B2B3…Bn叫正多边形A1A2…An的准位似图形,点A3称为准位似中心.
特例论证
(1)如图(2)已知正三角形A1A2A3的准位似图形为正三角形A1B2B3,试证明:随着点B2的运动,∠B3A3A1的大小始终不变.
数学思考
(2)如图(3)已知正方形A1A2A3A4的准位似图形为正方形A1B2B3B4,随着点B2的运动,∠B3A3A4的大小始终不变?若不变,请求出∠B3A3A4的大小;若改变,请说明理由.
归纳猜想
(3)在图(1)的情况下:
①试猜想∠B3A3A4的大小是否会发生改变?若不改变,请用含n的代数式表示出∠B3A3A4的大小(直接写出结果);若改变,请说明理由.
①∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠BnAnA1=___(用含n的代数式表示)
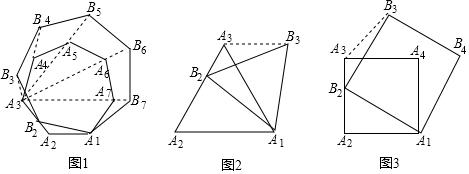
如图(1),在正多边形A1A2A3…An的边A2A3上任取一不与点A2重合的点B2,并以线段A1B2为边在线段A1A2的上方作以正多边形A1B2B3…Bn,把正多边形A1B2B3…Bn叫正多边形A1A2…An的准位似图形,点A3称为准位似中心.
特例论证
(1)如图(2)已知正三角形A1A2A3的准位似图形为正三角形A1B2B3,试证明:随着点B2的运动,∠B3A3A1的大小始终不变.
数学思考
(2)如图(3)已知正方形A1A2A3A4的准位似图形为正方形A1B2B3B4,随着点B2的运动,∠B3A3A4的大小始终不变?若不变,请求出∠B3A3A4的大小;若改变,请说明理由.
归纳猜想
(3)在图(1)的情况下:
①试猜想∠B3A3A4的大小是否会发生改变?若不改变,请用含n的代数式表示出∠B3A3A4的大小(直接写出结果);若改变,请说明理由.
①∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠BnAnA1=___(用含n的代数式表示)

▼优质解答
答案和解析
(1)证明:∵△A1A2A3与△A1B2B3是正三角形,
∴A1A2=A1A3,A1B2=A1B3,∠A2A1A3=∠B2A1B3=60°,
∴∠A2A1B2=∠A3A1B3,
∴△A2A1B2≌△A3A1B3,
∴∠B3A3A1=∠A2=60°,
∴∠B3A3A1的大小不变;
(2)∠B3A3A4的大小不变,
理由:如图,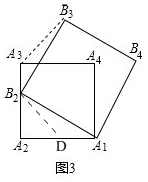 在边A1A2上取一点D,使A1D=A3B2,连接B2D,
在边A1A2上取一点D,使A1D=A3B2,连接B2D,
∵四边形A1A2A3A4与A1B2B3B4是正方形,
∴A1B2=B2B3,∠A1B2B3=∠A1A2A3=90°,
∴∠A3B2B3+∠A1B2A2=90°,∠A2A1B2+∠A1B2A2=90°,
∴∠A3B2B3=∠A2A1B2,
∴△A3B2B3≌△DA1B2,
∴∠B2A3B3=∠A1DB2,
∵A1A2=A2A3,A1D=A3B2,
∴A2B2=A2D,
∵∠A1A2A3=90°,
∴△DA2B2是等腰直角三角形,
∴∠A1DB2=135°,
∴∠B2A3B3=135°,
∵∠A4A3A2=90°,
∴∠B3A3A4=45°,
即:∠B3A3A4的大小始终不变;
(3)①∠B3A3B4的大小始终不变,理由:如图1,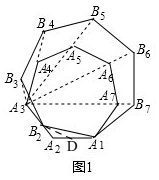
在A1A2上取一点D,使A1D=A3B2,
连接B2D,
∵∠A2A1B2=180°-∠A1B2A2,∠A3B2B3=180°-∠A1B2A2,
∴∠A2A1B2=∠A3B2B3,
∵A1B2=B2B3,
∴△A3B2B3≌△DA1B2,
∴∠B2A3B3=A1DB2,
∵A1A2=A2A3,A1D=A3B2,
∴A2D=A2B2,
∴∠A1DB2=
(180°-∠A1A2B2)=90°-
×
=90°-
∴∠B3A3A4=∠A1DB2-∠B2A3A4=90°-
-
=
;
②由①知,∠B3A3A4=
,
同①的方法可得,∠B4A4A5=
×2,∠B5A5A6=
×3,…,∠BnAnA1=
×(n-2),
∴①∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠BnAnA1
=
+
×2+
×3+…
×(n-2)=
,
故答案为
∴A1A2=A1A3,A1B2=A1B3,∠A2A1A3=∠B2A1B3=60°,
∴∠A2A1B2=∠A3A1B3,
∴△A2A1B2≌△A3A1B3,
∴∠B3A3A1=∠A2=60°,
∴∠B3A3A1的大小不变;
(2)∠B3A3A4的大小不变,
理由:如图,
 在边A1A2上取一点D,使A1D=A3B2,连接B2D,
在边A1A2上取一点D,使A1D=A3B2,连接B2D,∵四边形A1A2A3A4与A1B2B3B4是正方形,
∴A1B2=B2B3,∠A1B2B3=∠A1A2A3=90°,
∴∠A3B2B3+∠A1B2A2=90°,∠A2A1B2+∠A1B2A2=90°,
∴∠A3B2B3=∠A2A1B2,
∴△A3B2B3≌△DA1B2,
∴∠B2A3B3=∠A1DB2,
∵A1A2=A2A3,A1D=A3B2,
∴A2B2=A2D,
∵∠A1A2A3=90°,
∴△DA2B2是等腰直角三角形,
∴∠A1DB2=135°,
∴∠B2A3B3=135°,
∵∠A4A3A2=90°,
∴∠B3A3A4=45°,
即:∠B3A3A4的大小始终不变;
(3)①∠B3A3B4的大小始终不变,理由:如图1,

在A1A2上取一点D,使A1D=A3B2,
连接B2D,
∵∠A2A1B2=180°-∠A1B2A2,∠A3B2B3=180°-∠A1B2A2,
∴∠A2A1B2=∠A3B2B3,
∵A1B2=B2B3,
∴△A3B2B3≌△DA1B2,
∴∠B2A3B3=A1DB2,
∵A1A2=A2A3,A1D=A3B2,
∴A2D=A2B2,
∴∠A1DB2=
| 1 |
| 2 |
| 1 |
| 2 |
| 180°(n-2) |
| n |
| 90°(n-2) |
| n |
∴∠B3A3A4=∠A1DB2-∠B2A3A4=90°-
| 90°(n-2) |
| n |
| 180°(n-2) |
| n |
| 180° |
| n |
②由①知,∠B3A3A4=
| 180° |
| 2 |
同①的方法可得,∠B4A4A5=
| 180° |
| n |
| 180° |
| n |
| 180° |
| n |
∴①∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠BnAnA1
=
| 180° |
| n |
| 180° |
| n |
| 180° |
| n |
| 180° |
| n |
| 90°(n-1)(n-2) |
| n |
故答案为
|
作业帮用户
2018-01-05

 |
看了 阅读理解如图(1),在正多边...的网友还看了以下:
一段粗细不均匀的木棍如图所示,支在某点恰好平衡,若在该处将木棍截成两段,则所分成两段的重量必定是A 2020-04-27 …
正方体ABCD-A'B'C'D' EF分别为AA'.CC'的中点 P是CC'上的动点 过点EDP坐 2020-05-16 …
●采用(55)不会产生内部碎片。(55)A.分页存储管理 B.分段存储管理c.固定分区存储管理 D. 2020-05-26 …
戈森定理的内容为().A.边际效用递增规律B.边际效用递减规律C.边际效用相等规律D.边际效用平衡 2020-06-27 …
如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D 2020-07-21 …
只要公理,定理一边去!几何公理,欧氏几何公理,定理爬一边切,我不要证明,只要公理!所有的!你所说的 2020-07-30 …
下面定理中,没有逆定理的是A.两条直线被第三条直线所截,若同位角相等,则这两条直线平行B.线段垂直 2020-08-01 …
读了这段话,我看出了…………;周总理一边看,一边思索,也许他在想:…………他一句一句地审阅,看完一句 2020-11-02 …
考研政治现阶段如何复习?没有报班,现在政治主要复习什么?有去年的红宝书,可是怎么看红宝书?要边看边理 2020-11-03 …
把排列错误的句子整理成一段通顺的话在括号。小溪的两边,错落有致地分布着一个个小院落。我的家在把排列错 2021-01-13 …
 扫描下载二维码
扫描下载二维码