直二面角A-BD-C中，M、N分别是线段AB、CD上的点（不包括端点），且∠ADB=∠DBC=90°，AD=DB=BC=1，AM=DN，AM=x，MN=y．（1）若MN与平面BCD所成的角为45°，求x的值；（2）求函数y=f（x）的解析式

Question

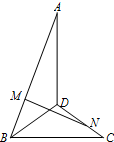直二面角A-BD-C中，M、N分别是线段AB、CD上的点（不包括端点），且∠ADB=∠DBC=90°，AD=DB=BC=1，AM=DN，AM=x，MN=y．
（1）若MN与平面BCD所成的角为45°，求x的值；
（2）求函数y=f（x）的解析式及定义域、值域．

Answer 1

分析：（1）作ME⊥BD于E，则ME⊥平面BCD，然后根据比例关系可得EN∥BC，然后根据ME=EN建立等式关系，求出x的值即可；（2）先利用勾股定理求出函数f（x）的解析式，然后根据偶次根式的意义求出定义域，根据二次函数的性质求出函数的值域．（1）作ME⊥BD于E，则ME⊥平面BCD，∴∠MNE=45°，DEEB=AMMB=DNNC⇒EN∥BC．ME=22(2-x)=1-22x，EN=22x，由ME=EN⇒x=22．（2）函数解析式y=f（x）=EM2+EN2=x2-2x+1=(x-22)2+12，定义域( 0 ， 2 )，值域[ 22 ， 1 )．点评：本题主要考查了立体几何，解题的关键是将空间问题转化成平面问题，属于中档题．