在直三棱柱ABC-A1B1C1中，AC=AA1=2，∠ACB=90°，点E，F分别是棱AB，BB1的中点，当二面角C1-AA1-B为45°时，直线EF与BC1的夹角为（）A.60°B.45°C.90°D.120°

Question

在直三棱柱ABC-A₁B₁C₁中，AC=AA₁=2，∠ACB=90°，点E，F分别是棱AB，BB₁的中点，当二面角C₁-AA₁-B为45°时，直线EF与BC₁的夹角为（　　）

A. 60°

B. 45°

C. 90°

D. 120°

Answer 1

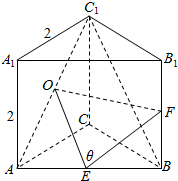由题意可得∠CAB=45°为二面角C₁-AA₁-B的平面角，△ABC为等腰直角三角形，
连AC₁，取AC₁得中点O，∵E，F分别是棱AB，BB₁的中点，∴OE平行且等于(1)/(2)BC₁，
∠OEF=θ或其补角，即为直线EF与BC₁的夹角．
由于OE=(1)/(2)BC₁=√(2)，EF=√(BF2+EB2)=√(1+2)=√(3)，OF=√(22+1)=√(5)，
由余弦定理可得cosθ=(OE2+EF2-OF2)/(2OE•EF)=0，
∴θ=90°，
故选：C．