在一个直角边长为10m的等腰直角三角形ABC的草地上，铺设一个也是等腰直角三角形PQR的花地，要求P，Q，R三点分别在△ABC的三条边上，且要使△PQR的面积最小，现有两种设计方案：方案-：直

Question

在一个直角边长为10m的等腰直角三角形ABC的草地上，铺设一个也是等腰直角三角形PQR的花地，要求P，Q，R三点分别在△ABC的三条边上，且要使△PQR的面积最小，现有两种设计方案：
方案-：直角顶点Q在斜边AB上，R，P分别在直角边AC，BC上；
方案二：直角顶点Q在直角边BC上，R，P分别在直角边AC，斜边AB上．请问应选用哪一种方案？并说明理由．

Answer 1

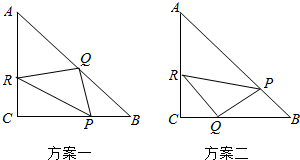
方案-：直角顶点Q在斜边AB上，R，P分别在直角边AC，BC上，则P，Q，R，C四点共圆，且AB与圆相切时△PQR的面积最小，最小面积为(1)/(2)×5×5=(25)/(2)；
方案二：直角顶点Q在直角边BC上，R，P分别在直角边AC，斜边AB上，设QP=QR=l，∠ORC=α，
∴2lsinα+lcosα=10，
∴l=(10)/(2sinα+cosα)=(10)/(√(5)sin(α+θ))≥(10)/(√(5))，
∴最小面积为(1)/(2)×((10)/(√(5)))2=10，
∵(25)/(2)>10，
∴应选用方案二．