早教吧作业答案频道 -->数学-->
如图,在几何体ABCDEF中,等腰梯形ABCD所在的平面与正方形CDEF所在的平面互相垂直,已知AB∥CD,AB=2BC=4,∠ABC=60°,点M是线段AC的中点.(Ⅰ)求证:CF⊥AD;(Ⅱ)求证:ME∥平面BCF;(Ⅲ
题目详情
如图,在几何体ABCDEF中,等腰梯形ABCD所在的平面与正方形CDEF所在的平面互相垂直,已知AB∥CD,AB=2BC=4,∠ABC=60°,点M是线段AC的中点.
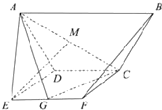
(Ⅰ)求证:CF⊥AD;
(Ⅱ)求证:ME∥平面BCF;
(Ⅲ)对于线段EF上的任意一点G,是否总有平面ACG⊥平面BCF,并说明理由.

(Ⅰ)求证:CF⊥AD;
(Ⅱ)求证:ME∥平面BCF;
(Ⅲ)对于线段EF上的任意一点G,是否总有平面ACG⊥平面BCF,并说明理由.
▼优质解答
答案和解析
证明:(Ⅰ)由正方形CDEF,得CF⊥CD,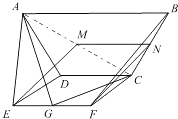
∵平面ABCD⊥平面CDEF,且平面ABCD∩平面CDEF=CD,
∴CF⊥平面ABCD,
又∵AD⊂平面ABCD,∴CF⊥AD.
(Ⅱ)如图,取BC中点N,连结MN、NF,
则MN∥AB,且MN=
AB=2,
又∵EF∥CD,CD∥AB,∴EF∥MN,
∵AB=2BC=4,∠ABC=60°,
∴CD=2,∴EF=MN,
∴四边形EFNM是平行四边形,∴ME∥FN,
又∵ME⊄平面EFNM,FN⊂平面BCF,
∴ME∥平面BCF.
(Ⅲ)对于线段EF上的任意一点G,总有平面ACG⊥平面BCF.
理由如下:
∵AB=2BC=4,∠ABC=60°,
在△ABC中,由余弦定理得:
AC2=AB2+BC2-2AB•BC•cos60°=16+4-2×4×2×cos60°=12,
∴AC=2
,∴AB2=AC2+BC2,∴AC⊥BC,
由(Ⅰ)知CF⊥平面ABCD,
∵AC⊂平面ABCD,∴CF⊥AC,
∵CF∩BC=C,且CF,BC⊂平面BCF,
∴AC⊥平面BCF,
又∵AC⊂平面ACG,∴平面ACG⊥平面BCF,
∴对于线段EF上的任意一点G,总有平面ACG⊥平面BCF.

∵平面ABCD⊥平面CDEF,且平面ABCD∩平面CDEF=CD,
∴CF⊥平面ABCD,
又∵AD⊂平面ABCD,∴CF⊥AD.
(Ⅱ)如图,取BC中点N,连结MN、NF,
则MN∥AB,且MN=
| 1 |
| 2 |
又∵EF∥CD,CD∥AB,∴EF∥MN,
∵AB=2BC=4,∠ABC=60°,
∴CD=2,∴EF=MN,
∴四边形EFNM是平行四边形,∴ME∥FN,
又∵ME⊄平面EFNM,FN⊂平面BCF,
∴ME∥平面BCF.
(Ⅲ)对于线段EF上的任意一点G,总有平面ACG⊥平面BCF.
理由如下:
∵AB=2BC=4,∠ABC=60°,
在△ABC中,由余弦定理得:
AC2=AB2+BC2-2AB•BC•cos60°=16+4-2×4×2×cos60°=12,
∴AC=2
| 3 |
由(Ⅰ)知CF⊥平面ABCD,
∵AC⊂平面ABCD,∴CF⊥AC,
∵CF∩BC=C,且CF,BC⊂平面BCF,
∴AC⊥平面BCF,
又∵AC⊂平面ACG,∴平面ACG⊥平面BCF,
∴对于线段EF上的任意一点G,总有平面ACG⊥平面BCF.
看了 如图,在几何体ABCDEF中...的网友还看了以下:
(1/2)将两个数a=17b=8,交换得a等于8,b等于17,下面语句正确的一组是?a,a等于b, 2020-04-26 …
关于比例的基本性质已知a比b等于c比d(b+或-d不等于0),求证:a+c比a-c等于b+d比b- 2020-05-16 …
已知a等于2015,b等于2016,c等于2017,求a2+b2+c2-ab-ac-bc的值错了错 2020-05-20 …
A等占百分比为百分之二十五,A等有多少人B等所占百分比为百分之五十,B等有多少人,C等有40人,C 2020-06-02 …
已知A等于{a,b,c},B等于{-1,0,1},f是A到的映射,则满足f(a)+f(b)+f(c 2020-06-23 …
a等于负六,b等于负二,c等于二十四点d为数轴上一点,他表示的数为x,求49/81(3x-a)^a 2020-07-17 …
在RT三角形ABC中,ab等于c,bc等于a,AC等于B,角c等于90度1已知a:b等于3:4,c 2020-07-22 …
一道大学线代问题已知向量a、b、c以及常数K、L、M满足阵Ka+Lb+Mc=0,KM≠0,则有?A 2020-07-27 …
二十二道π的数学口算题和一道圆的应用题1;c等于3.14d等于多少2;C等于6.28d等于多少3; 2020-07-31 …
有A1'B1'C1三个单元格,条件为如果B大于0,那么C等于A,如果B小于0,那么C等于A+...有 2020-10-31 …