早教吧作业答案频道 -->数学-->
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿
题目详情
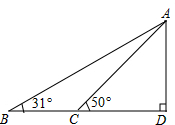
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
▼优质解答
答案和解析
(1)在Rt△ABD中,AD=24m,∠B=31°,
∴tan31°=
,即BD=
=40m,
在Rt△ACD中,AD=24m,∠ACD=50°,
∴tan50°=
,即CD=
=20m,
∴BC=BD-CD=40-20=20m,
则B,C的距离为20m;
(2)根据题意得:20÷2=10m/s<15m/s,
则此轿车没有超速.
∴tan31°=
| AD |
| BD |
| 24 |
| 0.6 |
在Rt△ACD中,AD=24m,∠ACD=50°,
∴tan50°=
| AD |
| CD |
| 24 |
| 1.2 |
∴BC=BD-CD=40-20=20m,
则B,C的距离为20m;
(2)根据题意得:20÷2=10m/s<15m/s,
则此轿车没有超速.
看了 据调查,超速行驶是引发交通事...的网友还看了以下:
10车从静止开始以1米每平方秒的加速度直线前进,车后面S=25M处与车开动的同时,某人以6M/S的 2020-05-13 …
汽车正在以10m/s的速度在平直的公路上前进突然发现前面s米处有一辆自行车以4米每秒的速度与汽车同 2020-05-15 …
如图所示,质量为0.5kg的物体在水平面成30°角的拉力F的作用下,沿水平桌面向右做直线运动,经过 2020-06-07 …
有一水平放置的平行平面玻璃板H,厚3.0cm,折射率n=1.5.在其下表面下2.0cm处有一小物S 2020-06-21 …
有些直接在后面加s的单词,可s的读音却不相同,有时读s,有时读z,有时读iz,请问该怎么区分阿, 2020-06-23 …
P是一个光屏,屏上有直径为5厘米的圆孔.Q是一块平面镜,与屏平行放置且相距10厘米.O1、02是过 2020-07-16 …
如图所示,质量为0.5kg的物体在与水平面成37度角的拉力F作用下,沿水平桌面向右作直线运动在线等 2020-07-17 …
P为椭圆面S:X^2+Y^2+Z^2-YZ=1上的动点,若S在点P处的切平面与XOY面垂直,求点P的 2020-11-01 …
用关联词连接下面的三句话1、安于平庸可能度过的是缺乏理想、碌碌无为的惨淡人生.2、失败往往能够成为我 2020-11-01 …
如何分清直接加S还是’S英文人名后面是否只能加’S,是不是没有直接加S这种说法的?eg:Timsgr 2020-11-05 …