早教吧作业答案频道 -->数学-->
如图(1)在平面六边形ABCDEF中,四边形ABCD是矩形,且AB=4,BC=2,AE=DE=2,BF=CF=5,点M,N分别是AD,BC的中点,分别沿直线AD,BC将△DEF,△BCF翻折成如图(2)的空间几何体ABCDEF.(1)利用下面
题目详情
如图(1)在平面六边形ABCDEF中,四边形ABCD是矩形,且AB=4,BC=2,AE=DE=
,BF=CF=
,点M,N分别是AD,BC的中点,分别沿直线AD,BC将△DEF,△BCF翻折成如图(2)的空间几何体ABCDEF.
(1)利用下面的结论1或结论2,证明:E、F、M、N四点共面;
结论1:过空间一点作已知直线的垂面,有且只有一个;
结论2:过平面内一条直线作该平面的垂面,有且只有一个.
(2)若二面角E-AD-B和二面角F-BC-A都是60°,求三棱锥E-BCF的体积.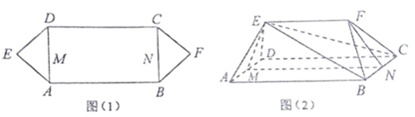
| 2 |
| 5 |
(1)利用下面的结论1或结论2,证明:E、F、M、N四点共面;
结论1:过空间一点作已知直线的垂面,有且只有一个;
结论2:过平面内一条直线作该平面的垂面,有且只有一个.
(2)若二面角E-AD-B和二面角F-BC-A都是60°,求三棱锥E-BCF的体积.

▼优质解答
答案和解析
证明:(1)由题意,点E在底面ABCD的射影在MN上,可设为点P,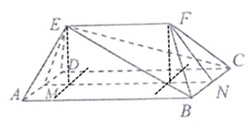
同理,点F在底面ABCD的射影在MN上,可设为点Q,
则EP⊥平面ABCD,FQ⊥平面ABCD,
∴平面EMP⊥平面ABCD,平面FNQ⊥平面ABCD,
又MN⊂平面ABCD,MN⊂平面EMP,MN⊂平面FNQ,
由结论2:过平面内一条直线作该平面的垂面,有且只有一个,
得到E、F、M、N四点共面.
(2)∵二面角E-AD-B和二面角F-BC-A都是60°,
∴∠EMP=∠FNQ=60°,∴EP=EM•sin60°=
,
∴三棱锥E-BCF的体积:
VE-BCF=VABCDEF-VE-ABCD
=2×
×(
×2)×
+(
×
×2)×3-
×(4×2)×
=
.

同理,点F在底面ABCD的射影在MN上,可设为点Q,
则EP⊥平面ABCD,FQ⊥平面ABCD,
∴平面EMP⊥平面ABCD,平面FNQ⊥平面ABCD,
又MN⊂平面ABCD,MN⊂平面EMP,MN⊂平面FNQ,
由结论2:过平面内一条直线作该平面的垂面,有且只有一个,
得到E、F、M、N四点共面.
(2)∵二面角E-AD-B和二面角F-BC-A都是60°,
∴∠EMP=∠FNQ=60°,∴EP=EM•sin60°=
| ||
| 2 |
∴三棱锥E-BCF的体积:
VE-BCF=VABCDEF-VE-ABCD
=2×
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
看了 如图(1)在平面六边形ABC...的网友还看了以下:
若数A/3与2A-3/3互为相反数,求A的相反数不相等的有理数A,B,C在数轴上的对应点分别为A, 2020-04-08 …
已知:P(A)=0.4P(B-A)=0.2P(-A+-B+C)=0.1求P(A+B+C)-A的-是 2020-04-25 …
A=B={(x,y)/x,y∈R}f是A到B的一个映射.并满足f:(x,y)→(-xy,x-y). 2020-04-26 …
a、b两车在公路上沿同一方向做直线运动,在t=0时刻,b车在a车前方500m处,它们的v-t图象如 2020-05-02 …
关于图中各点方向的判断,正确的是()A、a点在d点的东北方向B、b点在a点的东南方向C、c点在a点 2020-05-13 …
1.a,b两点在同一根纬线上,则a点在b的方向和b点在a的方向,只有在()中选出.A.南方和北方B 2020-05-13 …
设a表示一个两位数,b是一个3位数,现在把a放在b的左边,组成一个五位数为X,再把b放在a的左边, 2020-05-19 …
如图,A岛在C岛的南偏西58°,B岛在C岛的南偏东25°,B岛在A岛正东,求B岛看A'C两岛的视角 2020-06-06 …
(2010•长春三模)如图,A、B是两座现代化城市,C是一个古城遗址,C城在A城的北偏东30°,在 2020-06-12 …
如图,在海面上停着三艘船A、B、C,C船在A船的北偏西40゜方向,B船在A船的南偏西80゜方向,C 2020-06-12 …