早教吧作业答案频道 -->数学-->
已知△ABC和△ADE都是等边三角形,点B,D,E同一在一条直线上.(1)如图1,当AC⊥DE,且AD=2时,求线段BC的长度;(2)如图2,当且CD⊥BE时,取线段BC的中点F,线段DC的中点G,连接DF,EG,
题目详情
已知△ABC和△ADE都是等边三角形,点B,D,E同一在一条直线上.
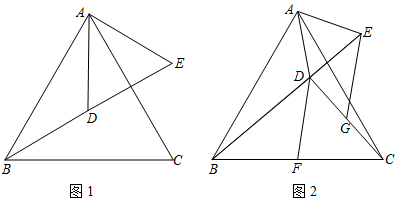
(1)如图1,当AC⊥DE,且 AD=2时,求线段BC的长度;
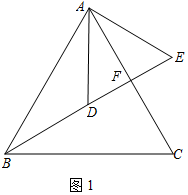
(2)如图2,当且CD⊥BE时,取线段BC的中点F,线段DC的中点G,连接DF,EG,求证:DF=EG.

(1)如图1,当AC⊥DE,且 AD=2时,求线段BC的长度;
(2)如图2,当且CD⊥BE时,取线段BC的中点F,线段DC的中点G,连接DF,EG,求证:DF=EG.
▼优质解答
答案和解析
 (1) 如图1所示:
(1) 如图1所示:
∵△ABC和△ADE都是等边三角形,AC⊥DE,AD=2,
∴BC=AC,DE=AD=2,DF=
DE=1,AF=CF,
∴AF=
=
,
∴AC=2AF=2
,
∴BC=2
;
(2)证明:连接CE,如图2所示:
∵ABC和△ADE都是等边三角形,点B,D,E同一在一条直线上.
∴AB=AC,AD=AE,∠BAC=∠DAE=∠AED=60°,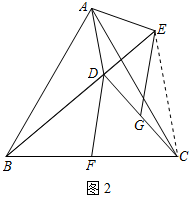
∴∠ADB=120°,∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠AEC=∠ADB=120°,
∴∠CED=∠AEC-∠AED=60°,
∵CD⊥BE,
∴∠DCE=30°,
∴DE=
CE,
∵线段BC的中点为F,线段DC的中点为G,
∴FG∥BD,FG=
BD,
∴FG∥DE,FG=DE,
∴四边形DFGE是平行四边形,
∴DF=EG.
 (1) 如图1所示:
(1) 如图1所示:∵△ABC和△ADE都是等边三角形,AC⊥DE,AD=2,
∴BC=AC,DE=AD=2,DF=
| 1 |
| 2 |
∴AF=
| AD2-DF2 |
| 3 |
∴AC=2AF=2
| 3 |
∴BC=2
| 3 |
(2)证明:连接CE,如图2所示:
∵ABC和△ADE都是等边三角形,点B,D,E同一在一条直线上.
∴AB=AC,AD=AE,∠BAC=∠DAE=∠AED=60°,

∴∠ADB=120°,∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴BD=CE,∠AEC=∠ADB=120°,
∴∠CED=∠AEC-∠AED=60°,
∵CD⊥BE,
∴∠DCE=30°,
∴DE=
| 1 |
| 2 |
∵线段BC的中点为F,线段DC的中点为G,
∴FG∥BD,FG=
| 1 |
| 2 |
∴FG∥DE,FG=DE,
∴四边形DFGE是平行四边形,
∴DF=EG.
看了 已知△ABC和△ADE都是等...的网友还看了以下:
设X是随机变量,C是常数,D(X)存在,试证:对于任意C≠E(X)必有E(X-C)^2>D(X). 2020-06-05 …
试证:当c=E(X)时,E(X-c)^2的值最小,并求出其最小值 2020-06-14 …
货币借贷活动是商品货币关系发展到一定阶段的必然产物。它是指()A.让渡货币在一段时间内的使用权B. 2020-06-20 …
下列句子中加点成语运用不正确的一项是()A.那里的天气变化无常,你可要多带些衣服B.现在的孩子对什 2020-06-27 …
对如图装置(铁的防护)的分析正确的是()A.甲装置是牺牲阳极的阴极保护法B.乙装置是牺牲阳极的阴极 2020-06-30 …
将过量的稀硫酸加入到有生锈铁钉的试管中,不能观察到的现象是()A.铁钉表面的锈迹消失,逐渐变得光亮 2020-07-10 …
用单侧光照射小麦的幼苗(如图所示).下列叙述错误的是()A.小麦幼苗接受单侧光刺激的部位在尖端B. 2020-07-15 …
如图是验证酶活性受pH影响的实验装置.下列叙述错误的是()A.实验原理之一是“新鲜土豆片含有过氧化 2020-07-23 …
将锌片和铜片按如图方式插入柠檬中,电流计指针发生偏转.则下列说法中正确的是()A.该装制能将电能转换 2020-10-29 …
图为番茄电池的示意图,下列说法正确的是()A.电流由锌通过导线流向铜B.负极反应为Zn-2e-=Zn 2020-11-01 …