早教吧作业答案频道 -->数学-->
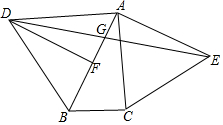
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABD和△ACE都是等边三角形,F为AB中点,DE交AB于点G求证:(1)DF=AC;(2)GD=GE.
题目详情
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABD和△ACE都是等边三角形,F为AB中点,DE交AB于点G
求证:(1)DF=AC;(2)GD=GE.
求证:(1)DF=AC;(2)GD=GE.

▼优质解答
答案和解析
证明:(1)∵∠ACB=90°,∠BAC=30°,
∴BC=
AB,∠ABC=60°,
∵F为AB中点,
∴BF=
AB,
∴BF=BC,
又∵△ABD是等边三角形,
∴BD=AB,∠ABD=60°,
在△DBF和△ABC中,
∵
,
∴△DBF≌△ABC,
∴DF=AC;
(2)∵△ACE为等边三角形,
∴AC=AE,∠CAE=60°,
又∵DF=AC,∠BAC=30°,
∴DF=EA,∠GAE=90°,
∵△ABD为等边三角形,且F为AB中点,
∴DF⊥AB,即∠DFG=90°,
在△DFG和△EAG中,
∵
,
∴△DFG≌△EAG(AAS),
∴DG=EG.
∴BC=
| 1 |
| 2 |
∵F为AB中点,
∴BF=
| 1 |
| 2 |
∴BF=BC,
又∵△ABD是等边三角形,
∴BD=AB,∠ABD=60°,
在△DBF和△ABC中,
∵
|
∴△DBF≌△ABC,
∴DF=AC;
(2)∵△ACE为等边三角形,
∴AC=AE,∠CAE=60°,
又∵DF=AC,∠BAC=30°,
∴DF=EA,∠GAE=90°,
∵△ABD为等边三角形,且F为AB中点,
∴DF⊥AB,即∠DFG=90°,
在△DFG和△EAG中,
∵
|
∴△DFG≌△EAG(AAS),
∴DG=EG.
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
如何解这类题已知A,B,C,D,E,F是含有同一种元素的化合物,其中F能使红色湿润石蕊试纸变蓝色, 2020-05-13 …
设有关系模式R(A,B,C,D,E,F),若有如下的函数依赖集F={A→B,(C,A)→D, (E, 2020-05-24 …
求助高一数学:两个事件E,F,P(F|E)=0.45,比较P(非F|E)与0.55的大小1.两个事 2020-06-10 …
若f(u)可导,且y=f(e^x),则有(),为什么A.dy=f'(e^x)dxB.dy=f'(e 2020-06-12 …
不定积分如果f(x)dx=F(x)+c,则∫e^-xf(e^-x)dx=?∫e^-xf(e^-x) 2020-06-20 …
某同学用显微镜观察洋葱鳞片叶内表皮细胞时看到了如图所示几幅图象,这几幅图象在操作过程中出现的顺序依 2020-07-01 …
问一道数学题,科大上p175我这样做的:(1)将等式两边求导:1=f`*e^f+f*e^f*f`= 2020-07-18 …
求证:(1)b=d,f=b^2;(2)求a,b,c,d,e,f,g的值(题目如下)设a、b、c、d 2020-07-27 …
如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,BF=DE 2020-11-03 …
如图中E、F、G为3个半透膜制成的透析袋,透析袋E中装有溶液甲,透析袋F和G中装有溶液乙.E、F、G 2020-11-26 …