早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角,AM是∠DAC的平分线,AC的垂直平分线与AM交于点F,与BC边交于点E,连接AE、CF.(1)补全图形;(2)判断四边形AECF的形状并加以证明.
题目详情
如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角,AM是∠DAC的平分线,AC的垂直平分线与AM交于点F,与BC边交于点E,连接AE、CF.
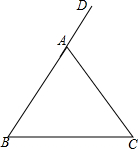
(1)补全图形;
(2)判断四边形AECF的形状并加以证明.

(1)补全图形;
(2)判断四边形AECF的形状并加以证明.
▼优质解答
答案和解析
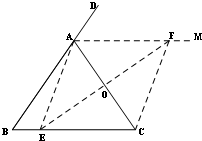 (1)如图所示:
(1)如图所示:
(2)猜想:四边形AECF是菱形,
证明:∵AB=AC,AM平分∠CAD,
∴∠B=∠ACB,∠CAD=2∠CAM,
∵∠CAD是△ABC的外角,
∴∠CAD=∠B+∠ACB,
∴∠CAD=2∠ACB,
∴∠CAM=∠ACB,
∴AF∥CE,
∴∠FAO=∠ACE
∵EF垂直平分AC,
∴OA=OC,∠AOF=∠COF=90°,
∴△AOF≌△COE,
∴AF=CE,
在四边形AECF中,AF∥CE,AF=CE,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形.
 (1)如图所示:
(1)如图所示:(2)猜想:四边形AECF是菱形,
证明:∵AB=AC,AM平分∠CAD,
∴∠B=∠ACB,∠CAD=2∠CAM,
∵∠CAD是△ABC的外角,
∴∠CAD=∠B+∠ACB,
∴∠CAD=2∠ACB,
∴∠CAM=∠ACB,
∴AF∥CE,
∴∠FAO=∠ACE
∵EF垂直平分AC,
∴OA=OC,∠AOF=∠COF=90°,
∴△AOF≌△COE,
∴AF=CE,
在四边形AECF中,AF∥CE,AF=CE,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
如图,读地质构造与地表形态图,同答下列问题.(1)从地质构造上看,c地属于构造,从地表形态上看,C 2020-04-06 …
1.如图,圆O1与圆O2内切与点P,圆O2的弦AB与圆O1相切于点Q,PQ连线与圆O2相交于R,连 2020-05-13 …
如图,在梯形ABCD中,AD//BC,E是边CD的中点,AE与BC的延长线交于点F.如图,在梯形A 2020-05-16 …
如图,△ABE与△ACD都是等边三角形,△AEC旋转后能与△ABD重合,EC与BD相交于点F,求如 2020-06-27 …
如图,四边形ABCD为轴对称图形,对称轴为直线MN,MN与AD相交于点M与BC交于点N,已知三角形 2020-07-17 …
如图三角形ABc中,外角AcD的平分线与角ABc的平分线交于A1,角ABc与AcD的平分线交于A2 2020-07-20 …
在设计图上,某城市中心有一个矩形广场,设计图的比例尺1:10000.图上矩形与实际矩形相似吗?如果 2020-07-27 …
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到B’的位置,AB’与CD交于点E.(1)试找出 2020-08-01 …
如图二次函数y=-2x的2次方+4X+6的图像与X轴交于点A,B,且与Y轴交于点C,(1)求点A, 2020-08-02 …
关于创建图表,下列说法中()是错误的A。创建图表除了嵌入式图表,图形图表之外,还可手工绘制。B。嵌入 2020-11-03 …