早教吧作业答案频道 -->数学-->
(本题证明值可直接利用如下结论:若公共边所对的两个张角相等,则相应的四点共圆.例如如图1,由∠ACB=∠ADB,可得四点A、B、C、D共圆)如图2,圆内接五边形ABCDE中,AD是外接圆的直径
题目详情
(本题证明值可直接利用如下结论:若公共边所对的两个张角相等,则相应的四点共圆.例如如图1,由∠ACB=∠ADB,可得四点A、B、C、D共圆)如图2,圆内接五边形ABCDE中,AD是外接圆的直径,BE⊥AD,垂足为H,过点H作平行于CE的直线,与直线AC,DC分别交于F,G.证明:
(1)点A,B,F,H共圆;
(2)四边形BFCG是矩形.
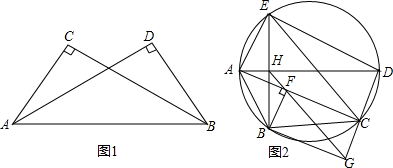
(1)点A,B,F,H共圆;
(2)四边形BFCG是矩形.

▼优质解答
答案和解析
证明:(1)由HG∥CE,得∠BHF=∠BEC,
又∵
=
,
∴∠BAF=∠BEC,
∴∠BAF=∠BHF,
∴点A、B、F、H共圆;
(2)由(1)的结论,得∠BHA=∠BFA,
∵BE⊥AD,
∴BF⊥AC,
又∵AD是圆的直径,
∴CG⊥AC,
由A、B、C、D共圆及A、B、F、H共圆,
∴∠BFG=∠DAB=∠BCG,
∴B、G、F、H共圆,
∴∠BGC=∠AFB=90°,
∴BG⊥GC,
∴四边形BFCG是矩形.
又∵
 |
| BC |
 |
| BC |
∴∠BAF=∠BEC,
∴∠BAF=∠BHF,
∴点A、B、F、H共圆;
(2)由(1)的结论,得∠BHA=∠BFA,
∵BE⊥AD,
∴BF⊥AC,
又∵AD是圆的直径,
∴CG⊥AC,
由A、B、C、D共圆及A、B、F、H共圆,
∴∠BFG=∠DAB=∠BCG,
∴B、G、F、H共圆,
∴∠BGC=∠AFB=90°,
∴BG⊥GC,
∴四边形BFCG是矩形.
看了 (本题证明值可直接利用如下结...的网友还看了以下:
以下说法错误的是().一般在哈夫曼树中,权值越大的叶子离根结点越近b哈夫曼树中没有度数为1的分支结 2020-06-23 …
和平共处五项原则的提出开拓了我国外交的新局面,下列哪一项不是和平共处五项原则的内容()A.互不侵犯 2020-06-30 …
谁会这道题:由我国提出的解决国与由我国提出的解决国与国之间问题的基本准则是[]A、和平共处五项原则 2020-07-05 …
为集中全力纠正博古等人的“左倾”军事路线错误,会议委托张闻天起草《中央关于反对敌人五次“围剿”的总 2020-07-06 …
20世纪80年代以来,我国外交的主要特点是()A.奉行独立自主的和平外交政策B.坚持和平共处五项原则 2020-11-04 …
校讯通3、张阿姨去年共结余6万元,她准备把其中的40%存入银行,如果存三年,年利率是3.45%,存五 2020-11-10 …
把毛泽东思想和邓小平理论确立为中国共产党的指导思想的会议分别是A.遵义会议和中共十五大B.中共七大和 2020-11-13 …
中共十五届四中全会通过的《中共中央关于国有企业改革和发展若干重大问题的决定》指出:从战略上调整国有经 2020-12-03 …
“共争青岛归还;同看国贼罢黜”这是一幅欢庆五四运动取得胜利的对联.五四运动的胜利标志着中国()A.旧 2020-12-26 …
20世纪50年代,中国在接见印度代表团时首次提出,后来成为处理国与国关系的基本准则是()A.“求同存 2021-01-16 …