早教吧作业答案频道 -->数学-->
D为等腰Rt△ABC斜边BC上一点(不与B、C重合),DE⊥BC于点D,交直线BA于点E,作∠EDF=45°,DF交AC于F,连接EF,BD=nDC,当n=时,△DEF为等腰直角三角形.
题目详情
D为等腰Rt△ABC斜边BC上一点(不与B、C重合),DE⊥BC于点D,交直线BA于点E,作∠EDF=45°,DF交AC于F,连接EF,BD=nDC,当n=___时,△DEF为等腰直角三角形.
▼优质解答
答案和解析
 分两种情况:
分两种情况:
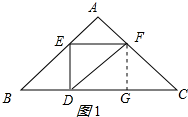
①当∠DEF=90°时,如图1所示:
∵DE⊥BC,
∴∠BDE=90°=∠DEF,
∴EF∥BC,
作FG⊥BC于G,
∵△ABC是等腰直角三角形,
∴△CFG、△BDE是等腰直角三角形,四边形EFGD是正方形,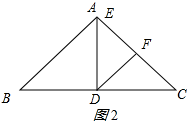
∴BD=DE=EF=DG=FG=CG,
∴BD=
CD,
∴n=
;
②当∠EFD=90°时,如图2所示:
∵∠EDF=45°,
∴∠DEF=45°,此时E与A重合,D是BC的中点,
∴BD=CD,
∴n=1.
故答案为:
或1.
 分两种情况:
分两种情况:①当∠DEF=90°时,如图1所示:
∵DE⊥BC,
∴∠BDE=90°=∠DEF,
∴EF∥BC,
作FG⊥BC于G,
∵△ABC是等腰直角三角形,
∴△CFG、△BDE是等腰直角三角形,四边形EFGD是正方形,

∴BD=DE=EF=DG=FG=CG,
∴BD=
| 1 |
| 2 |
∴n=
| 1 |
| 2 |
②当∠EFD=90°时,如图2所示:
∵∠EDF=45°,
∴∠DEF=45°,此时E与A重合,D是BC的中点,
∴BD=CD,
∴n=1.
故答案为:
| 1 |
| 2 |
看了 D为等腰Rt△ABC斜边BC...的网友还看了以下:
圆心角(2) (17 20:49:12)O的半径OC,OD与弦AB交于点E,F,且AE=BF.求证 2020-05-13 …
1EF是平行四边形ABCD的对角线AC的垂直平分线,与边AD,BC分别交于点E,F,垂足为O,求证 2020-05-15 …
如图①,四边形ABCD是平行四边形,对角线AC,BD相交于点O,过点O做直线EF分别交AD,BC于 2020-05-15 …
在平行四边形ABCD中,过对角线AC的中点O作直线EF分别与AD,BC交于点E,F.连结BEAF在 2020-05-16 …
探索如图,画∠AOB=120°及角平分线OC,把三角形的60°角的顶点放在OC上一点D处,绕点D旋 2020-06-02 …
已知AB‖CD,直线EF分别交AB,CD于点E,F,角∠BEF的平行线宇∠DEF的平行线相较于点F 2020-06-24 …
1ab等于ac,角a等于36度,ab得中垂线mn交ac于点d,交ab于点m,求证bd是角abc的平 2020-07-30 …
如何求证C,D,E,F四点共圆.以知:圆1与圆2相交与点A,B,点P在BA的延长线上,割线PCD交 2020-07-31 …
△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,过点P作BC的平行线交AB,AC于 2020-08-03 …
1.如图1,已知角ABC=45度,P为角ABC内部一点,PE//AB,PF//BC,分别交BC.BA 2020-11-03 …