早教吧作业答案频道 -->数学-->
如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.(1)求证:CF=BF;(2)若△CFB是等腰直角三角形,则∠DAE+∠DEA等于多少度?
题目详情
如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.
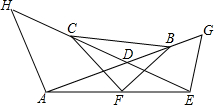
(1)求证:CF=BF;
(2)若△CFB是等腰直角三角形,则∠DAE+∠DEA等于多少度?

(1)求证:CF=BF;
(2)若△CFB是等腰直角三角形,则∠DAE+∠DEA等于多少度?
▼优质解答
答案和解析
(1)证明:连接AC,BE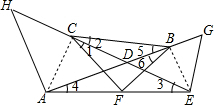 ,
,
∵△ADH是等腰三角形,C是DH中点,
∴AC⊥DH,
同理BE⊥DG,
在RT△ACE中,∵F是斜边AE中点,
∴FC=
AE=EF
∴∠1=∠3
同理BF=
AE=AF
∴CF=BF;
(2) ∵BF=AF,CF=EF,
∴∠4=∠6,∠3=∠1,
∴∠3+∠4=∠1+∠6,
∵∠BDC=∠ADE,
∴∠2+∠5=∠3+∠4,
∴∠1+∠6=∠2+∠5,
∵△BCF为等腰直角三角形,
∴∠1+∠2+∠5+∠6=45°+45°=90°,
∴∠1+∠6=∠2+∠5=45°,
∴∠3+∠4=45°,
即∠DAE+∠DEA=45°.
 ,
,∵△ADH是等腰三角形,C是DH中点,
∴AC⊥DH,
同理BE⊥DG,
在RT△ACE中,∵F是斜边AE中点,
∴FC=
| 1 |
| 2 |
∴∠1=∠3
同理BF=
| 1 |
| 2 |
∴CF=BF;
(2) ∵BF=AF,CF=EF,
∴∠4=∠6,∠3=∠1,
∴∠3+∠4=∠1+∠6,
∵∠BDC=∠ADE,
∴∠2+∠5=∠3+∠4,
∴∠1+∠6=∠2+∠5,
∵△BCF为等腰直角三角形,
∴∠1+∠2+∠5+∠6=45°+45°=90°,
∴∠1+∠6=∠2+∠5=45°,
∴∠3+∠4=45°,
即∠DAE+∠DEA=45°.
看了 如图,已知AG与HE相交于点...的网友还看了以下:
肼(N2H4)常用于火箭或原电池的燃料.己知:①N2(g)+2O2(g)═2NO2(g)△H=+6 2020-04-07 …
已知:①C(s)+O2(g)=CO2(g);△H=-393.5kJ•mol1②2CO(g)+O2 2020-04-07 …
已知:2CO(g)+O2(g)=2CO2(g)ΔH="-566"kJ·mol-1N2(g)+O2( 2020-04-07 …
有三个函数f(x)=tan(x+pi/4),g(x)=(1+tanx)(1-tanx),h(x)= 2020-05-17 …
阱(N2H4)常用于火箭或原电池的燃料.己知:①N2(g)+2O2(g)=2NO2(g)△H=+6 2020-06-21 …
炽热的炉膛内有反应:C(s)+O2(g)CO2(g)ΔH=-392kJ·mol-1,往炉膛内通入水 2020-07-19 …
导数题设f(5)=5,f'(5)=3,g(5)=4,g'(5)=1在下列情况下求h(5)和h'(5 2020-07-30 …
甲醇质子交换膜燃料电池中将甲醇蒸气转化为氢气的两种反应原理是:①CH3OH(g)+H2O(g)═CO 2020-11-13 …
甲醇质子交换膜燃料电池中将甲醇蒸气转化为氢气的两种反应原理是:①CH3OH(g)+H2O(g)=CO 2020-11-13 …
甲醇质子交换膜燃料电池中将甲醇蒸气转化为氢气的两种反应原理是:①CH3OH(g)+H2O(g)=CO 2020-11-13 …